题目内容
二进制数111011（2）对应的十进制数 ．
考点：进位制
专题：计算题
分析：欲将二进制数111011（2）用十进制表示，只须根据转换公式：1×25+1×24+1×23+0×22+1×21+1进行计算即得．
解答：
解：二进制数111011（2）用十进制可以表示为：
1×25+1×24+1×23+0×22+1×21+1=59．
故答案为：59．
1×25+1×24+1×23+0×22+1×21+1=59．
故答案为：59．
点评：本题主要考查了算法的概念以及二进制数与用十进制的互化，属于基础题．
练习册系列答案
相关题目
已知椭圆
+
=1（a＞b＞0），过焦点F1的弦AB的长是2，另一焦点为F2，则△ABF2的周长是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| A、2a | B、4a-2 |
| C、4a | D、4a+4 |
圆心角为1rad，半径为1的扇形的面积为（ ）
| A、1 | ||
B、
| ||
C、
| ||
| D、π |
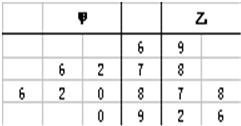如图是甲、乙两名同学的六次测试成绩的茎叶图，下列说法正确的是（ ）①甲同学成绩的中位数大于乙同学成绩的中位数；
②甲同学的平均分比乙同学平均分高；
③甲同学成绩的平均分比乙同学平均分低；
④甲同学成绩的方差小于乙同学成绩的方差．
| A、①③ | B、①②④ | C、③④ | D、③ |