题目内容
1.若f(x)的定义域为{x∈R|x≠0},满足f(x)-2f($\frac{1}{x}$)=3x,则f(x)为( )| A. | 偶函数 | B. | 奇函数 | C. | 既奇又偶函数 | D. | 非奇非偶函数 |
分析 由f(x)-2f($\frac{1}{x}$)=3x,把$\frac{1}{x}$代换x可得:f($\frac{1}{x}$)-2f(x)=$\frac{3}{x}$,联立消去f($\frac{1}{x}$)可得:f(x),即可判断出奇偶性.
解答 解:由f(x)-2f($\frac{1}{x}$)=3x,
把$\frac{1}{x}$代换x可得:f($\frac{1}{x}$)-2f(x)=$\frac{3}{x}$,
联立消去f($\frac{1}{x}$)可得:f(x)=-x-$\frac{2}{x}$,x∈{x∈R|x≠0}.
∵f(-x)=x+$\frac{2}{x}$=-f(x),
∴f(x)是奇函数.
故选:B.
点评 本题考查了函数的解析式、函数奇偶性的判定方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
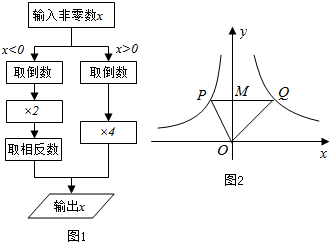
12.根据图1所示的程序,得到了y与x的函数图象,如图2.若点M是y轴正半轴上任意一点,过点M作PQ∥x轴交图象于点P,Q,连接OP,OQ.则以下结论:
①x<0 时,y=$\frac{2}{x}$
②△OPQ的面积为定值.
③x>0时,y随x的增大而增大.
④MQ=2PM.
⑤∠POQ可以等于90°.其中正确结论是( )
①x<0 时,y=$\frac{2}{x}$
②△OPQ的面积为定值.
③x>0时,y随x的增大而增大.
④MQ=2PM.
⑤∠POQ可以等于90°.其中正确结论是( )

| A. | ①②④ | B. | ②④⑤ | C. | ③④⑤ | D. | ②③⑤ |
