题目内容
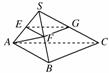
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知AD=4,BD=4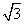 ,AB=2CD=8.
,AB=2CD=8.
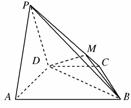
(1)设M是PC上的一点,证明:平面MBD⊥平面PAD;
(2)当M点位于线段PC什么位置时,PA∥平面MBD?
(3)求四棱锥P-ABCD的体积.
解析: (1)证明:在△ABD中,
∵AD=4,BD=4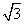 ,AB=8,∴AD2+BD2=AB2.
,AB=8,∴AD2+BD2=AB2.
∴AD⊥BD.
又平面PAD⊥平面ABCD,
平面PAD∩平面ABCD=AD,BD⊂平面ABCD,
∴BD⊥平面PAD.
又BD⊂平面MBD,∴平面MBD⊥平面PAD.
(2)当M点位于线段PC靠近C点的三等分点处时,
PA∥平面MBD.
证明如下:连接AC,交BD于点N,连接MN.
∵AB∥DC,∴四边形ABCD是梯形.
∵AB=2CD,
∴CN∶NA=1∶2.
又∵CM∶MP=1∶2,∴CN∶NA=CM∶MP,∴PA∥MN.
∵MN⊂平面MBD,PA⊄平面MBD,∴PA∥平面MBD.
(3)过点P作PO⊥AD交AD于O,
∵平面PAD⊥平面ABCD,∴PO⊥平面ABCD.
即PO为四棱锥P-ABCD的高.
又△PAD是边长为4的等边三角形,∴PO=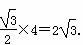
在Rt△ADB中,斜边AB上的高为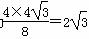 ,此即为梯形ABCD的高.
,此即为梯形ABCD的高.
梯形ABCD的面积SABCD=
四棱锥P-ABCD的体积VP-ABCD=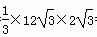 =24.
=24.

练习册系列答案
相关题目
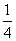 B.
B.
 ≥0的解集为________.
≥0的解集为________.
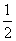 ,
,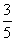 ,
,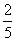 ,审核过关后,甲,乙,丙三人文化测试合格的概率分别为
,审核过关后,甲,乙,丙三人文化测试合格的概率分别为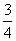 。
。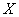 ,求
,求