题目内容
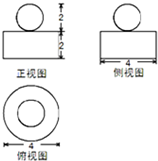
如图是一个几何体的三视图,根据图中数据,可得该几何体的体积是 .(注:V球=R3)

考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:由已知中的三视图可得,该几何体是一个圆柱和球的组合体,分别计算出体积后,相加可得答案.
解答:
解:由已知中的三视图可得,该几何体是一个圆柱和球的组合体,
其中球的直径为2,即球的半径为1,
则球的体积V球=
πr3=
π,
圆柱的底面直径为4,即底面半径为2,高为2,
则圆柱的体积V柱=Sh=π•22•2=8π,
故组合体的体积V=V球+V柱=
π,
故答案为:
π
其中球的直径为2,即球的半径为1,
则球的体积V球=
| 4 |
| 3 |
| 4 |
| 3 |
圆柱的底面直径为4,即底面半径为2,高为2,
则圆柱的体积V柱=Sh=π•22•2=8π,
故组合体的体积V=V球+V柱=
| 28 |
| 3 |
故答案为:
| 28 |
| 3 |
点评:本题考查的知识点是由三视图求体积,其中根据已知的三视图分析出几何体的形状是解答的关键.

练习册系列答案
相关题目
在△ABC中,a,b,c分别是角A,B,C的对边,且a:b:c=
:1:2,则角B为( )
| 3 |
| A、30° | B、60° |
| C、90° | D、120° |
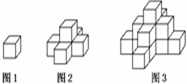 如图1是一个水平摆放的小正方体木块,图2、图3是由这样的小正方体木块叠放而成,按照这样的规律继续逐个叠放下去,那么在第七个叠放的图形中小正方体木块数应是
如图1是一个水平摆放的小正方体木块,图2、图3是由这样的小正方体木块叠放而成,按照这样的规律继续逐个叠放下去,那么在第七个叠放的图形中小正方体木块数应是