题目内容
设等差数列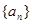 的公差
的公差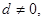 且
且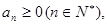 记
记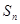 为数列
为数列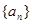 的前
的前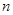 项和.
项和.
(1)若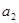 、
、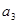 、
、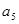 成等比数列,且
成等比数列,且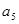 、
、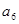 的等差中项为
的等差中项为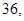 求数列
求数列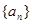 的通项公式;
的通项公式;
(2)若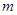 、
、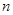 、
、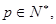 且
且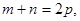 证明:
证明: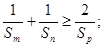
(3)若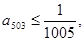 证明:
证明: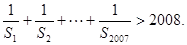
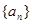 的公差
的公差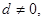 且
且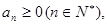 记
记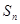 为数列
为数列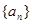 的前
的前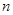 项和.
项和.(1)若
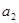 、
、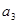 、
、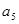 成等比数列,且
成等比数列,且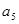 、
、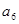 的等差中项为
的等差中项为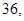 求数列
求数列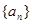 的通项公式;
的通项公式;(2)若
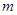 、
、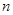 、
、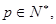 且
且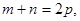 证明:
证明: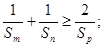
(3)若
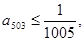 证明:
证明: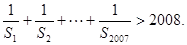
(1)由已知得 即
即
化简得:


而 即
即
故 分
分
(2)易知等差数列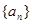 的首项
的首项 不妨设
不妨设

因为


 分
分
(3)
而


 即
即
化简得:



而
 即
即
故
 分
分(2)易知等差数列
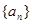 的首项
的首项 不妨设
不妨设

因为



 分
分(3)

而



略

练习册系列答案
相关题目
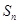 是等差数列
是等差数列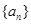
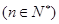 ,的前
,的前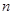 项和,且
项和,且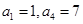 ,则
,则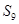 = .
= . 行”.从上往下数,第
行”.从上往下数,第 个
个 ,第
,第 个
个
 是递增数列,且满足
是递增数列,且满足
 项公式;
项公式; ,求数列
,求数列 的前
的前 项和
项和 .
.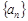 中,
中,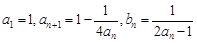 ,其中
,其中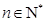 .
.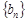 为等差数列;
为等差数列;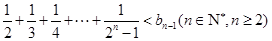
 的前
的前 项和为
项和为 ,已知
,已知 N
N ).
). 与
与 之间插入n个数,使这n+2个数组成公差为
之间插入n个数,使这n+2个数组成公差为 的等差数列,求数列
的等差数列,求数列 的前
的前 .
.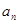 }是公差不为零的等差数列,
}是公差不为零的等差数列,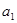 =1,且
=1,且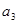 ,
,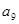 成等比数列.
成等比数列.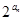 }的前
}的前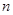 项和
项和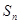 .
.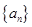 中
中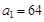 ,公比
,公比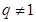 ,且
,且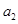 ,
,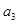 ,
,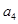 分别为某等差数列的第5项,第3项,第2项.
分别为某等差数列的第5项,第3项,第2项.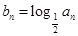 ,求数列
,求数列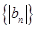 的前
的前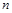 项和
项和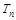 .
. 中,若
中,若 则
则 = .
= .