题目内容
已知R为全集，A={x|log2（3-x）≤2}，
，求（CRA）∩B．
解：由log2（3-x）≤2=log24，因为y=log2x为增函数，所以
，解得-1≤x＜3，
所以A={x|-1≤x＜3}，
于是CRA={x|x＜-1，或 x≥3}．…（7分）
又由
，
而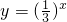
为减函数，所以 x+1≥0，
解得x≥-1，所以B={x|x≥-1}．…（10分）
故有（CRA）∩B={x|x≥3}．…（12分）
分析：指数函数、对数函数的单调性和特殊点求出集合A 和集合B，从而求得CRA，进而求得（CRA）∩B．
点评：本题主要考查指数函数、对数函数的单调性和特殊点，集合的补集，两个集合的交集的定义和求法，属于中档题．
，解得-1≤x＜3，所以A={x|-1≤x＜3}，
于是CRA={x|x＜-1，或 x≥3}．…（7分）
又由
，而
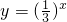为减函数，所以 x+1≥0，解得x≥-1，所以B={x|x≥-1}．…（10分）
故有（CRA）∩B={x|x≥3}．…（12分）
分析：指数函数、对数函数的单调性和特殊点求出集合A 和集合B，从而求得CRA，进而求得（CRA）∩B．
点评：本题主要考查指数函数、对数函数的单调性和特殊点，集合的补集，两个集合的交集的定义和求法，属于中档题．
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
百分学生作业本题练王系列答案
相关题目
已知R为全集，A={x|log
(3-x)≥-2}，B={y|y=2x，x∈R}，则（CRA）∩B=（ ）
| 1 |
| 2 |
| A、φ |
| B、（0，+∞） |
| C、（-∞，-1）∪（0，+∞） |
| D、[3，+∞） |