题目内容
解下列问题:(1)已知a>0,b>0,且4a+b=1,求ab的最大值;
(2)已知x>2,求x+
 的最小值;
的最小值;
【答案】分析:(1)根据基本不等式的性质可知4a+b≥2 ,进而求得
,进而求得 的最大值.
的最大值.
(2)先把x+ 整理成x-2+
整理成x-2+ +2,进而利用基本不等式求得x+
+2,进而利用基本不等式求得x+ 的最小值.
的最小值.
解答:解:(1)∵a>0,b>0,4a+b=1,
∴1=4a+b≥2 =4
=4 ,
,
当且仅当4a=b= ,即a=
,即a= ,b=
,b= 时,等号成立.
时,等号成立.
∴ ≤
≤ ,
,
∴ab≤ .
.
所以ab的最大值为 .
.
(2)∵x>2,
∴x-2>0,
∴x+ =x-2+
=x-2+ +2
+2
≥2 +2=6,
+2=6,
当且仅当x-2= ,即x=4时,等号成立.
,即x=4时,等号成立.
所以x+ 的最小值为6.
的最小值为6.
点评:本题主要考查了运用基本不等式求最值.运用基本不等式要注意把握住“一定二正三相等”的原则.
 ,进而求得
,进而求得 的最大值.
的最大值.(2)先把x+
 整理成x-2+
整理成x-2+ +2,进而利用基本不等式求得x+
+2,进而利用基本不等式求得x+ 的最小值.
的最小值.解答:解:(1)∵a>0,b>0,4a+b=1,
∴1=4a+b≥2
 =4
=4 ,
,当且仅当4a=b=
 ,即a=
,即a= ,b=
,b= 时,等号成立.
时,等号成立.∴
 ≤
≤ ,
,∴ab≤
 .
.所以ab的最大值为
 .
.(2)∵x>2,
∴x-2>0,
∴x+
 =x-2+
=x-2+ +2
+2≥2
 +2=6,
+2=6,当且仅当x-2=
 ,即x=4时,等号成立.
,即x=4时,等号成立.所以x+
 的最小值为6.
的最小值为6.点评:本题主要考查了运用基本不等式求最值.运用基本不等式要注意把握住“一定二正三相等”的原则.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
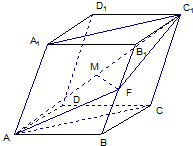 已知四棱柱ABCD-A1B1C1D1中的底面是菱形,且∠DAB=∠A1AB=∠A1AD=60°,AD=1,AA1=a,F为棱BB的中点,M为线段AC的中点.设
已知四棱柱ABCD-A1B1C1D1中的底面是菱形,且∠DAB=∠A1AB=∠A1AD=60°,AD=1,AA1=a,F为棱BB的中点,M为线段AC的中点.设 (2009•淮安模拟)如图,已知正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点,试用空间向量知识解下列问题:
(2009•淮安模拟)如图,已知正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点,试用空间向量知识解下列问题: