题目内容
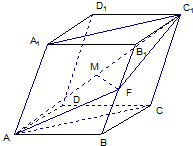已知四棱柱ABCD-A1B1C1D1中的底面是菱形，且∠DAB=∠A1AB=∠A1AD=60°，AD=1，AA1=a，F为棱BB的中点，M为线段AC的中点．设| AB |
| e1 |
| AD |
| e2 |
| AA1 |
| e3 |
（1）求证：直线MF∥平面ABCD；
（2）求证：直线MF⊥面A1ACC1；
（3）是否存在a，使平面AFC1与平面ABCD所成二面角的平面角是30°？如果存在，求出相应的a 值，如果不存在，请说明理由．（提示：可设出两面的交线）
分析：（1）由：|
|=|
|=1，|
|=a，
•
=
，
•
=
•
=
a，
=
=
a，
=
+
+
，
=
（
+
+
），
=
+
=
+
=
+
，
=
-
=
（
-
），
=
-
=
-
=2
，由此能证明直线MF∥平面ABCD．
（2）由
•
=（
-
）•
=0，
•
=（
-
）（
+
+
）•
=0，知MF⊥AA1，MF⊥AC，AC和AA1是面ABCD内的相交直线，由此能证明直线MF⊥面A1ACC1．
（3）设平面AFC1与平面ABCD的交线为c，两平面有一个公共点A，故A在直线c上；MF在面AFC1内，直线MF∥平面ABCD，有MF∥直线c，由直线MF⊥面A1ACC1，直线AC和直线AC1在平面A1ACC1内，知平面AFC1与平面ABCD所成二面角的平面角是∠C1AC由此能推导出不存在这样的a值，使平面AFC1与平面ABCD所成二面角的平面角是30°．
| e1 |
| e2 |
| e3 |
| e 1 |
| e2 |
| 1 |
| 2 |
| e1 |
| e3 |
| e2 |
| e3 |
| 1 |
| 2 |
| e1 |
| e3 |
| e2 |
| e3 |
| 1 |
| 2 |
| AC1 |
| e1 |
| e2 |
| e3 |
| AM |
| 1 |
| 2 |
| e1 |
| e2 |
| e3 |
| AF |
| AB |
| BF |
| AB |
| 1 |
| 2 |
| AA1 |
| e1 |
| 1 |
| 2 |
| e3 |
| MF |
| AF |
| AM |
| 1 |
| 2 |
| e1 |
| e2 |
| DB |
| AB |
| AD |
| e1 |
| e2 |
| MF |
（2）由
| MF |
| AA1 |
| e1 |
| e2 |
| 1 |
| 2 |
| e3 |
| MF |
| AC |
| e1 |
| e2 |
| e1 |
| e2 |
| e3 |
| 1 |
| 2 |
（3）设平面AFC1与平面ABCD的交线为c，两平面有一个公共点A，故A在直线c上；MF在面AFC1内，直线MF∥平面ABCD，有MF∥直线c，由直线MF⊥面A1ACC1，直线AC和直线AC1在平面A1ACC1内，知平面AFC1与平面ABCD所成二面角的平面角是∠C1AC由此能推导出不存在这样的a值，使平面AFC1与平面ABCD所成二面角的平面角是30°．
解答：（1）证明：|
|=|
|=1，
|
|=a，
•
=
，
•
=
•
=
a，（2分）
=
+
+
，
=
（
+
+
），
=
+
=
+
=
+
，
=
-
=
（
-
），（3分）
=
-
=
-
=2
，
DB在面ABCD内，MF在面ABCD外，
∴直线MF∥平面ABCD；（4分）
（2）证明：
•
=（
-
）•
=0，（5分）
•
=（
-
）•（
+
+
）•
=0，（6分）
∴MF⊥AA1，MF⊥AC，AC和AA1是面ABCD内的相交直线，
∴直线MF⊥面A1ACC1；（7分）
（3）解：设平面AFC1与平面ABCD的交线为c，两平面有一个公共点A，
∴A在直线c上；MF在面AFC1内，直线MF∥平面ABCD，有MF∥直线c，
由2）知，直线MF⊥面A1ACC1，直线AC和直线AC1在平面A1ACC1内，
∴MF⊥AC1，MF⊥AC，因此，有AC1⊥直线c，AC⊥直线c，
平面AFC1与平面ABCD所成二面角的平面角是∠C1AC，（10分）
假设存在这样的a，使∠C1AC=30°，
则cos30°=cos＜
，
＞
=
| e1 |
| e2 |
|
| e3 |
| e 1 |
| e2 |
| 1 |
| 2 |
| e1 |
| e3 |
| e2 |
| e3 |
| 1 |
| 2 |
| AC1 |
| e1 |
| e2 |
| e3 |
| AM |
| 1 |
| 2 |
| e1 |
| e2 |
| e3 |
| AF |
| AB |
| BF |
| AB |
| 1 |
| 2 |
| AA1 |
| e1 |
| 1 |
| 2 |
| e3 |
| MF |
| AF |
| AM |
| 1 |
| 2 |
| e1 |
| e2 |
| DB |
| AB |
| AD |
| e1 |
| e2 |
| MF |
DB在面ABCD内，MF在面ABCD外，
∴直线MF∥平面ABCD；（4分）
（2）证明：
| MF |
| AA1 |
| e1 |
| e2 |
| 1 |
| 2 |
| e3 |
| MF |
| AC |
| e1 |
| e2 |
| e1 |
| e2 |
| e3 |
| 1 |
| 2 |
∴MF⊥AA1，MF⊥AC，AC和AA1是面ABCD内的相交直线，
∴直线MF⊥面A1ACC1；（7分）
（3）解：设平面AFC1与平面ABCD的交线为c，两平面有一个公共点A，
∴A在直线c上；MF在面AFC1内，直线MF∥平面ABCD，有MF∥直线c，
由2）知，直线MF⊥面A1ACC1，直线AC和直线AC1在平面A1ACC1内，
∴MF⊥AC1，MF⊥AC，因此，有AC1⊥直线c，AC⊥直线c，
平面AFC1与平面ABCD所成二面角的平面角是∠C1AC，（10分）
假设存在这样的a，使∠C1AC=30°，
则cos30°=cos＜
| AC 1 |
| AC |
=
|
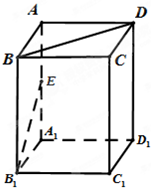已知四棱柱ABCD-A1B1C1D1的底面是边长为1的正方形，侧棱垂直底边ABCD四棱柱，AA1=2，E是侧棱AA1的中点，求
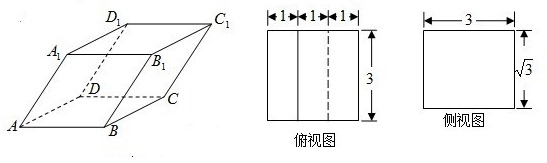（2012•江门一模）如图，已知四棱柱ABCD-A1B1C1D1的俯视图是边长为3的正方形，侧视图是长为3宽为
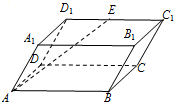如图，已知四棱柱ABCD-A1B1C1D1的底面ABCD是矩形，AB=4，AA1=3，∠BAA1=60°，E为棱C1D1的中点，则