题目内容

7．已知某几何体的三视图如图所示，则该几何体的体积是2$\sqrt{3}$+π．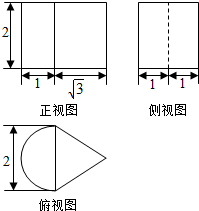

分析 该几何体是由半个圆柱与一个三棱柱拼接而成，代入柱体体积公式，可得答案．

解答 解：该几何体是由半个圆柱（该圆柱的底面圆半径是1，高是2）与一个三棱柱（该棱柱的底面面积等于$\frac{1}{2}$×2×$\sqrt{3}=\sqrt{3}$，高是2）拼接而成，
其体积等于$\frac{1}{2}$×π×12×2+$\frac{1}{2}$×2×$\sqrt{3}$×2=2$\sqrt{3}$+π，
故答案为：2$\sqrt{3}$+π．

点评 本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．

练习册系列答案
相关题目
9．集合M由9个互不相同的小球构成，小球上分别标有号码1，2，…，9，其中奇数号小球为黑色，偶数号小球为红色．对于M的子集A，如果它包含的小球号码具有如下性质：“若2k∈A，则2k-1∈A且2k+1∈A，k∈Z”，就称A为达标子集，那么集合M恰好包含2个红球的达标子集个数为18．
18．某四棱锥的三视图如图所示，则该四棱锥的体积是（　　）
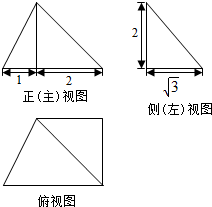
A．$5\sqrt{3}$B．2$\sqrt{3}$C．$\frac{{5\sqrt{3}}}{3}$D．$\frac{2\sqrt{3}}{3}$
15．已知双曲线C：$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{8}$=1的左右焦点分别为F1、F2，若双曲线C的右支上存在一点P，使得（$\overrightarrow{OP}$+$\overrightarrow{O{F}_{2}}$）•$\overrightarrow{{F}_{2}P}$=0，O为坐标原点，且|$\overrightarrow{P{F}_{1}}$|=λ|$\overrightarrow{P{F}_{2}}$|，则实数λ等于（　　）
A．4B．2C．$\sqrt{3}$D．$\sqrt{2}$
2．函数y=$\sqrt{a-{a}^{x}}$（a＞0，a≠1）的定义域和值域都是[0，1]，则loga$\frac{5}{6}$+loga$\frac{48}{5}$=（　　）
A．1B．2C．3D．4
12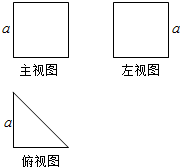．已知某个几何体的三视图如图，其中主视图和左视图（侧视图）都是边长为a的正方形，俯视图是直角边长为a的等腰直角三角形，则此几何体的表面积为（　　）
A．（3+$\sqrt{2}$）a2B．4a2C．（4+$\sqrt{2}$）a2D．3$\sqrt{2}$a2
19．一个几何体的三视图如图所示，若该几何体的体积为$\frac{10}{3}$，则a•b2的值为4．
16．方程x-lg$\frac{1}{x}$-3=0的解所在的区间为（　　）
A．（0，1）B．（1，2）C．（2，3）D．（3，+∞）
17．“m＞1”是“函数f（x）=m+log2x（x≥1）不存在零点”的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分又不必要条件

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网