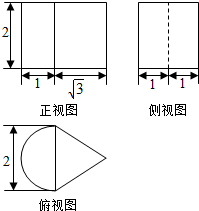
题目内容

12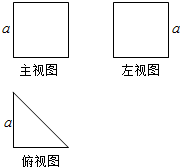．已知某个几何体的三视图如图，其中主视图和左视图（侧视图）都是边长为a的正方形，俯视图是直角边长为a的等腰直角三角形，则此几何体的表面积为（　　）
A．（3+$\sqrt{2}$）a2B．4a2C．（4+$\sqrt{2}$）a2D．3$\sqrt{2}$a2

分析 根据几何体的三视图，得出该几何体是直三棱柱，结合图中数据即可求出它的表面积．

解答 解：根据几何体的三视图，得；
该几何体是一个三棱柱，且上、下底面为腰长是a的等腰直角三角形，
侧面由两个边长为a的正方形和一个边长为a和$\sqrt{2}$a的长方形组成，
所以，该几何体的表面积为
2×$\frac{1}{2}$a2+a2×2+$\sqrt{2}$a2=（3+$\sqrt{2}$）a2．
故选：A．

点评 本题考查了利用空间几何体的三视图求表面积的应用问题，是基础题目．

练习册系列答案
相关题目
2．如图1，已知正方体ABCD-A1B1ClD1的棱长为a，动点M、N、Q分别在线段PM上．当三棱锥Q-BMN的俯视图如图2所示时，三棱锥Q-BMN的正视图面积等于（　　）
A．$\frac{1}{2}$a2B．$\frac{1}{4}$a2C．$\frac{\sqrt{2}{a}^{2}}{4}$D．$\frac{\sqrt{3}{a}^{2}}{4}$
3．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）经过点A（2，1），离心率为$\frac{\sqrt{2}}{2}$，过点B（3，0）的直线l与椭圆C交于不同的两点M，N．
（1）求椭圆C的方程；
（2）求$\overrightarrow{BM}$•$\overrightarrow{BN}$的取值范围．
20．在平面直角坐标系xOy中，已知直线y=x与圆心在第二象限的圆C相切于原点O，且圆C与圆C′：x2+y2-2x-2y-6=0的面积相等．
（Ⅰ）求圆C的标准方程；
（Ⅱ）试探究圆C上是否存在异于原点的点Q，使点Q到定点F（4，0）的距离等于线段OF的长？若存在，求出点Q的坐标；若不存在，请说明理由．
7．已知某几何体的三视图如图所示，则该几何体的体积是2$\sqrt{3}$+π．
17．如图是一个空间几何体的三视图，则该几体体的外接球的体积是（　　）
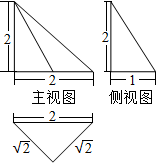
A．$\frac{64\sqrt{2}}{3}$πB．$\frac{32\sqrt{2}}{3}$πC．$\frac{8\sqrt{2}}{3}$πD．8π
4．在平面直角坐标系xOy中，直线l的参数方程为$\left\{\begin{array}{l}x=t+3\\ y=3-t\end{array}\right.$（参数t∈R），圆C的参数方程为$\left\{\begin{array}{l}x=2cosθ\\ y=2sinθ+2\end{array}\right.$（参数θ∈[0，2π）），圆心到直线l的距离为2$\sqrt{2}$．
1．要从5名男生，3名女生中选出3人作为学生代表参加社区活动，且女生人数不多于男生人数，那么不同的选法种数有40种．
2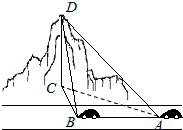．如图，有一辆汽车在一条水平的公路上向正西行驶，汽车在A点测得公路北侧山顶D的仰角为30°，汽车行驶300m后到达B点测得山顶D恰好在正北方，且仰角为45°，则山的高度CD为（　　）
A．150$\sqrt{2}$B．150$\sqrt{3}$C．300$\sqrt{2}$D．300$\sqrt{3}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网