题目内容
2.函数y=$\sqrt{a-{a}^{x}}$(a>0,a≠1)的定义域和值域都是[0,1],则loga$\frac{5}{6}$+loga$\frac{48}{5}$=( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据函数定义域和值域的关系,判断函数的单调性,结合对数的运算法则进行求解即可.
解答 解:当x=1时,y=0,则函数为减函数,故a>1,
则当x=0时,y=1,
即y=$\sqrt{a-1}$=1,即a-1=1,则a=2,
则loga$\frac{5}{6}$+loga$\frac{48}{5}$=loga($\frac{5}{6}$•$\frac{48}{5}$)=log28=3,
故选:C.
点评 本题主要考查对数的基本运算以及函数定义域和值域的应用,比较基础.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.若log2a,log2b是方程x2+x-3=0的两根,则(lg$\frac{a}{b}$)2等于( )
| A. | 13 | B. | 13(lg2)2 | C. | 10 | D. | 10(lg2) |
13.如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为( )
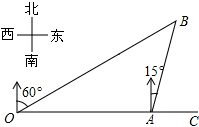

| A. | 4km | B. | 2$\sqrt{3}$km | C. | 2$\sqrt{2}$km | D. | ($\sqrt{3}$+1)km |
17.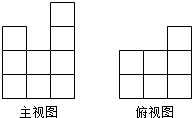 用大小和形状完全相同的小正方体木块搭成一个几何体,使得它的主视图和俯视图如图所示,则搭成这样的一个几何体至少需要小正方体木块的个数为( )
用大小和形状完全相同的小正方体木块搭成一个几何体,使得它的主视图和俯视图如图所示,则搭成这样的一个几何体至少需要小正方体木块的个数为( )
 用大小和形状完全相同的小正方体木块搭成一个几何体,使得它的主视图和俯视图如图所示,则搭成这样的一个几何体至少需要小正方体木块的个数为( )
用大小和形状完全相同的小正方体木块搭成一个几何体,使得它的主视图和俯视图如图所示,则搭成这样的一个几何体至少需要小正方体木块的个数为( )| A. | 22个 | B. | 19个 | C. | 16个 | D. | 13个 |
14.双曲线x2-y2=1右支上一点P(a,b)到直线l:y=x的距离d=$\sqrt{2}$.则a+b=( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{2}$或-$\frac{1}{2}$ | D. | 2或-2 |