题目内容
平行于直线2x-y+3=0且过点（-2，-4）的直线l与函数g（x）=x2图象所围成的图形的面积等于________．
分析：先求直线l的方程，再确定积分区间与被积函数，即可求得面积．
解答：设直线l方程为2x-y+c=0
∵直线l过（-2，-4）点
∴-4+4+c=0
∴c=0
∴直线l方程为2x-y=0
与函数g（x）=x2联立，可得交点坐标为（0，0），（2，0）
∴直线l与函数g（x）=x2图象所围成的图形的面积等于
=（
）
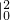=4-
=故答案为：
点评：本题考查定积分在求面积中的应用，确定积分区间与被积函数是关键．
练习册系列答案
相关题目
若直线l：x+ay+2=0平行于直线2x-y+3=0，则直线l在两坐标轴上截距之和是（ ）
| A、6 | B、2 | C、-1 | D、-2 |
平行于直线2x-y+1=0且与圆x2+y2=5相切的直线的方程是（ ）
| A、2x-y+5=0 | B、x2-y-5=0 | C、2x+y+5=0或2x+y-5=0 | D、2x-y+5=0或2x-y-5=0 |