题目内容
11.若复数z满足$\frac{(2+i)^{2}}{z}$=i,则z=4-3i.分析 由$\frac{(2+i)^{2}}{z}$=i,得$z=\frac{(2+i)^{2}}{i}$,再利用复数代数形式的乘除运算化简即可得答案.
解答 解:由$\frac{(2+i)^{2}}{z}$=i,
得z=$\frac{(2+i)^{2}}{i}=\frac{3+4i}{i}=\frac{-i(3+4i)}{-{i}^{2}}=4-3i$.
故答案为:4-3i.
点评 本题考查了复数代数形式的混合运算,是基础题.

练习册系列答案
相关题目
1.下列函数中,既是偶函数又在区间(0,+∞)上单调递增的是( )
| A. | $y=\frac{1}{x}$ | B. | y=lgx | C. | y=|x|-1 | D. | $y={({\frac{1}{2}})^{lnx}}$ |
19.已知函数f(x)=$\frac{{{e^x}+{e^{-x}}+sinx}}{{{e^x}+{e^{-x}}}}$,其导函数记为f′(x),则f(2016)+f′(2016)+f(-2016)-f′(-2016)=( )
| A. | 2016 | B. | 0 | C. | 1 | D. | 2 |
16.给出定义:设f′(x)是函数y=f(x)的导函数,f″(x)是函数f′(x)的导函数,若方程f″(x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”.已知函数f(x)=3x+4sinx-cosx的拐点是M(x0,f(x0)),则点M( )
| A. | 在直线y=-3x上 | B. | 在直线y=3x上 | C. | 在直线y=-4x上 | D. | 在直线y=4x上 |
3.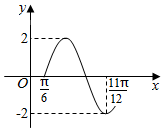 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,$|φ|<\frac{π}{2}$)的部分图象如图所示,则f(x)的递增区间为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,$|φ|<\frac{π}{2}$)的部分图象如图所示,则f(x)的递增区间为( )
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,$|φ|<\frac{π}{2}$)的部分图象如图所示,则f(x)的递增区间为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,$|φ|<\frac{π}{2}$)的部分图象如图所示,则f(x)的递增区间为( )| A. | $({-\frac{π}{12}+2kπ,\frac{5π}{12}+2kπ})$,k∈Z | B. | $({-\frac{π}{12}+kπ,\frac{5π}{12}+kπ})$,k∈Z | ||
| C. | $({-\frac{π}{6}+2kπ,\frac{5π}{6}+2kπ})$,k∈Z | D. | $({-\frac{π}{6}+kπ,\frac{5π}{6}+kπ})$,k∈Z |
20.已知$\frac{π}{2}<α<π$且$sin(α+\frac{π}{6})=\frac{3}{5}$,则$cos(α-\frac{π}{6})$等于( )
| A. | $\frac{{-4-3\sqrt{3}}}{10}$ | B. | $\frac{{4+3\sqrt{3}}}{10}$ | C. | $\frac{{4-3\sqrt{3}}}{10}$ | D. | $\frac{{3\sqrt{3}-4}}{10}$ |
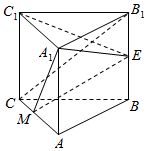 如图.在三棱柱ABC-A1B1C1中,已知侧棱与底面垂直,∠CAB=90°,且AC=1,AB=2,E为BB1的中点,M为AC上一点,$\overrightarrow{AM}$=$\frac{2}{3}$$\overrightarrow{AC}$.
如图.在三棱柱ABC-A1B1C1中,已知侧棱与底面垂直,∠CAB=90°,且AC=1,AB=2,E为BB1的中点,M为AC上一点,$\overrightarrow{AM}$=$\frac{2}{3}$$\overrightarrow{AC}$.