Question

【题目】如图，已知正方形和矩形所在平面互相垂直， ， ．

（1）求二面角的大小；

（2）求点到平面的距离.

Answer 1

【答案】（1）60°．（2）．

【解析】试题分析：（1）先根据条件建立空间直角坐标系，设各点坐标，根据方程组求各面法向量，再根据向量数量积求夹角，最后根据二面角与向量夹角关系得结果（2）根据向量投影得点到平面的距离为再根据向量数量积求值

试题解析： 正方形和矩形所在平面互相垂直，

分别以AB，AD，AF为x，y，z轴建立空间直角坐标系，

则A（0，0，0），B（，0，0）， C（， ，0）， D（0， ，0），

E（, ，1），F（0，0，1）．

（1）设平面CDE的法向量为平面BDE的法向量，

由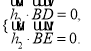 解得.

∴ ，

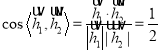∴ 二面角 B—DE—C等于60°．

（2）

，

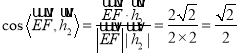．设点到平面BDF的距离为h，则

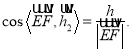
∴．所以点F到平面BDE的距离为．