题目内容
已知扇形的面积为S，当扇形的中心角为多少弧度时，扇形的周长最小？并求出此最小值．
[解析] 解法1：设l为扇形的弧长，由S＝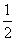
l·r
得l＝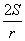
，故扇形的周长C＝2r＋.
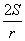即2r2－C·r＋2S＝0.由于r存在，故方程有解，
因此有Δ＝C2－16S≥0，即C≥4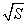
.
∴周长C的最小值为4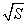.此时，r＝
＝，
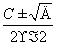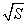中心角α＝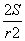
＝2rad
所以当扇形的中心角为2rad时，扇形的周长最小，最小值为4.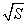
解法2：设l为扇形的弧长，由S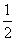＝l·r得l＝，
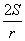故扇形的周长C＝2r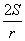＋≥2
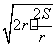＝4.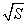
当且仅当2r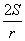＝，即S＝r2时取“＝”，
此时，α＝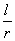
＝＝
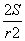＝2rad.
所以当扇形的中心角为2rad时，扇形的周长最小，最小值为4.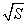
练习册系列答案
相关题目
＋α)＝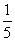
，那么cosα＝( )
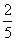B．－
，且α在第四象限，计算：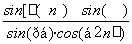
(n∈Z)．
，
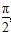)的图像如图所示，为了得到函数g(x)＝sin2x的图像，则只需将f(x)的图像( )
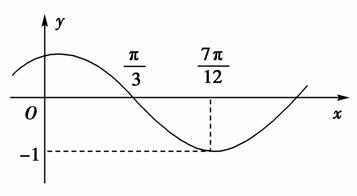
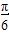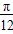个长度单位
个长度单位