题目内容
设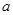 为实数,函数
为实数,函数 。
。
(1)若 ,求
,求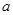 的取值范围;
的取值范围;
(2)求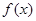 的最小值;
的最小值;
(3)设函数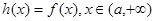 ,直接写出(不需给出演算步骤)不等式
,直接写出(不需给出演算步骤)不等式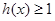 的解集.
的解集.
(1)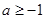 ;(2)
;(2)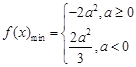 ;(3)当
;(3)当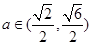 时,解集为
时,解集为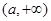 ;当
;当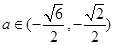 时,解集为
时,解集为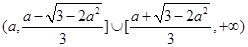 ;当
;当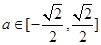 时,解集为
时,解集为
解析试题分析:(1)由 ,结合解析式得
,结合解析式得 ,分
,分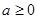 和
和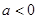 两种情况即可求
两种情况即可求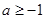 ;
;
(2)由已知函数解析式可分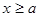 和
和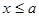 两种情况分别得
两种情况分别得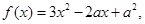 和
和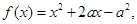 结合二次函数的图像和单调性可得
结合二次函数的图像和单调性可得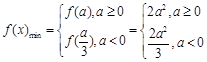 和
和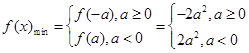 ,从而有
,从而有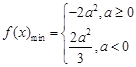 ;(3)结合二次函数的图像和一元二次不等式解集直接写出即可.
;(3)结合二次函数的图像和一元二次不等式解集直接写出即可.
试题解析: (1)若 ,则
,则 1分
1分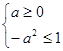 或
或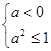 2分
2分 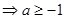 3分
3分
(2)当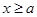 时,
时,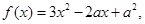
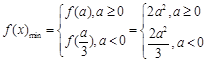 5分
5分
当 时,
时,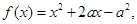
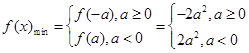 7分
7分
综上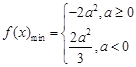 8分
8分
(3)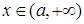 时,
时,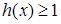 得,
得,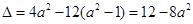
当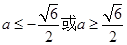 时,
时,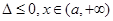 ; 10分
; 10分
当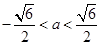 时,△>0,得:
时,△>0,得: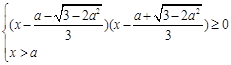 11分
11分
讨论得:当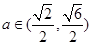 时,解集为
时,解集为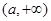 ; 12分
; 12分
当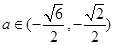 时,解集为
时,解集为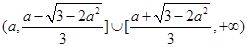 ; 13分
; 13分
当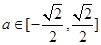 时,解集为
时,解集为 . 14分
. 14分
考点:1.考查函数的概念、性质、图象;2.解一元二次不等式;3.运用数形结合、分类讨论的思想方法进行探索、分析与解决问题的综合能力

练习册系列答案
相关题目
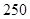 万元,每生产
万元,每生产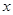 千件,需另投入成本为
千件,需另投入成本为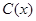 .当年产量不足
.当年产量不足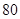 千件时,
千件时,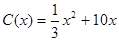 (万元).当年产量不小于
(万元).当年产量不小于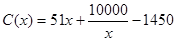 (万元).每件商品售价为
(万元).每件商品售价为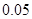 万元.通过市场分析,该厂生产的商品能全部售完.
万元.通过市场分析,该厂生产的商品能全部售完.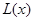 (万元)关于年产量
(万元)关于年产量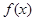 若存在
若存在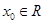 ,使得
,使得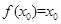 成立,则称
成立,则称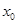 为
为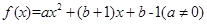
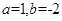 时,求函数
时,求函数 的不动点;
的不动点;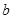 ,函数
,函数 的取值范围;
的取值范围;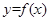 图象上
图象上 、
、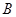 两点的横坐标是函数
两点的横坐标是函数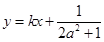 对称,求
对称,求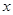 (元)与年产量
(元)与年产量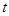 (吨)满足函数关系
(吨)满足函数关系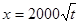 .若工厂每生产一吨产品必须赔付农场
.若工厂每生产一吨产品必须赔付农场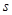 元(以下称
元(以下称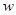 (元)表示为年产量
(元)表示为年产量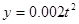 (元),在工厂按照获得最大利润的产量进行生产的前提下,农场要在索赔中获得最大净收入,应向张林的工厂要求赔付价格
(元),在工厂按照获得最大利润的产量进行生产的前提下,农场要在索赔中获得最大净收入,应向张林的工厂要求赔付价格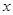 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为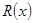 万元,且
万元,且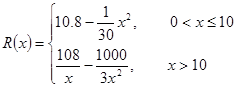 .
.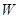 (万元)关于年产量
(万元)关于年产量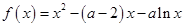 .
. 的单调区间
的单调区间 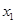 、
、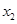 ,且
,且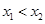 ,求证:
,求证: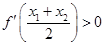 .
. 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为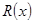 万元,且
万元,且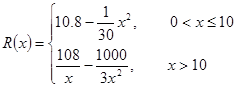 .
.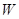 (万元)关于年产量
(万元)关于年产量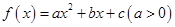 ,当
,当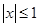 时,
时,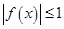 .
.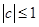 ;
;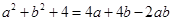 成立,请先求出
成立,请先求出 的值,并利用
的值,并利用 的表达式.
的表达式. 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为 万元,且
万元,且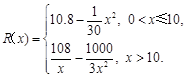
 (万元)关于年产量
(万元)关于年产量