题目内容
已知幂函数 为偶函数,且在区间
为偶函数,且在区间 上是单调增函数
上是单调增函数
(1)求函数 的解析式;
的解析式;
(2)设函数 ,其中
,其中 .若函数
.若函数 仅在
仅在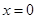 处有极值,求
处有极值,求 的取值范围.
的取值范围.
(1) ;(2)
;(2) .
.
解析试题分析:(1)根据函数的单调性分析出指数大于零,解不等式可得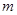 的取值范围,再利用
的取值范围,再利用 得
得 ,然后根据幂函数
,然后根据幂函数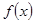 为偶函数可得
为偶函数可得 ;(2)根据导数求极值,为使方程
;(2)根据导数求极值,为使方程 只有
只有 一个根,则必须
一个根,则必须 恒成立,于是根据判别式可求.
恒成立,于是根据判别式可求.
试题解析:(1) 在区间
在区间 上是单调增函数,
上是单调增函数,
即
 又
又 4分
4分
而 时,
时, 不是偶函数,
不是偶函数, 时,
时, 是偶函数,
是偶函数, . 6分
. 6分
(2) 显然
显然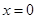 不是方程
不是方程 的根.
的根.
为使 仅在
仅在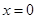 处有极值,必须
处有极值,必须 恒成立, 8分
恒成立, 8分
即有 ,解不等式,得
,解不等式,得 . 11分
. 11分
这时, 是唯一极值.
是唯一极值. 
 . 12分
. 12分
考点:1.幂函数;2.函数的单调性;3.导数公式;4.函数的极值.

练习册系列答案
相关题目
 m,盖子边长为
m,盖子边长为 m,
m,
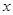 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为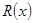 万元,且
万元,且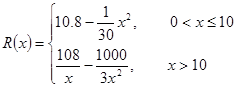 .
.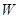 (万元)关于年产量
(万元)关于年产量 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为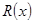 万元,且
万元,且 .
.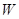 (万元)关于年产量
(万元)关于年产量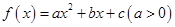 ,当
,当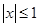 时,
时,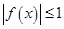 .
.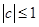 ;
;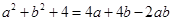 成立,请先求出
成立,请先求出 的值,并利用
的值,并利用 的表达式.
的表达式. (升)关于行驶速度
(升)关于行驶速度 (千米/每小时)的函数解析式可以表示为
(千米/每小时)的函数解析式可以表示为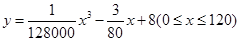 ,已知甲、乙两地相距100千米.
,已知甲、乙两地相距100千米.
 在
在 上为增函数,求实数
上为增函数,求实数 的取值范围;
的取值范围; 时,方程
时,方程 有实根,求实数
有实根,求实数 的最大值.
的最大值.
 .
. 在定义域上为增函数,求实数
在定义域上为增函数,求实数 的取值范围;
的取值范围; 上的最小值.
上的最小值.