题目内容
过双曲线
-
=1的右焦点F2,倾斜角为30°的直线交双曲线于A、B两点,则|AB|= .
| x2 |
| 3 |
| y2 |
| 6 |
考点:双曲线的简单性质
专题:计算题,空间位置关系与距离
分析:确定直线AB的方程,代入双曲线方程,求出A,B的坐标,即可求线段AB的长.
解答:
解:由双曲线的方程得F1(-3,0),F2(3,0),直线AB的方程为y=
(x-3)①
将其代入双曲线方程消去y得,5x2+6x-27=0,解之得x1=-3,x2=
.
将x1,x2代入①,得y1=-2
,y2=-
故|AB|=
.
故答案为:
.
| ||
| 3 |
将其代入双曲线方程消去y得,5x2+6x-27=0,解之得x1=-3,x2=
| 9 |
| 5 |
将x1,x2代入①,得y1=-2
| 3 |
2
| ||
| 5 |
故|AB|=
| 16 |
| 5 |
| 3 |
故答案为:
| 16 |
| 5 |
| 3 |
点评:本题考查直线与双曲线的位置关系,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
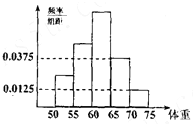 为了了解某市今年准备报考体育专业的学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,则第2小组的频率为
为了了解某市今年准备报考体育专业的学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,则第2小组的频率为