题目内容
8.设函数g(x)=ex+2x-a(a∈R,e为自然对数底数),定义在R上函数f(x)满足:f(-x)+f(x)=x2,且当x<0时,f′(x)<x,若存在x0∈{x|f(x)+$\frac{1}{2}$≥f(1-x)+x}.使g[g(x0)]=x0,则实数a的取值范围为a≤$\sqrt{e}$+$\frac{1}{2}$.分析 构造新的函数,将f(x)转化为可以知道性质的函数,将x0的范围确定出来,再处理g(x),由性质确定出a的范围.
解答 解:∵f(-x)+f(x)=x2
∴令F(x)=f(x)-$\frac{1}{2}{x}^{2}$,
∴f(x)-$\frac{1}{2}{x}^{2}$=-f(-x)+$\frac{1}{2}$x2
∴F(x)=-F(-x),即F(x)为奇函数,
∵F′(x)=f′(x)-x,
且当x<0时,f′(x)<x,
∴F′(x)<0对x<0恒成立,
∵F(x)为奇函数,
∴F(x)在R上单调递减,
∵f(x)+$\frac{1}{2}$≥f(1-x)+x,
∴f(x)+$\frac{1}{2}$-$\frac{1}{2}{x}^{2}$≥f(1-x)+x-$\frac{1}{2}{x}^{2}$,
即F(x)≥F(1-x),
∴x≤1-x,
x0≤$\frac{1}{2}$,
由g[g(x0)]=x0可得g(x0)=g-1(x0),
而g(x)如果与其反函数相交,则交点一定在直线y=x上,
故有g(x0)=x0,
即h(x)=ex+x-a=0在(-∞,$\frac{1}{2}$]有解.
∵h′(x)=ex+1,
∴h(x)在R上单调递增.
∴h(x)max=h($\frac{1}{2}$)=$\sqrt{e}$+$\frac{1}{2}$-a≥0即可,
∴a≤$\sqrt{e}$+$\frac{1}{2}$.
点评 本题考查对f(x)那个式子的处理,重新构造新的函数,通过新函数确定x0的范围,再来确定a的范围.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
19.直线y=$\frac{1}{2}$x+b是曲线y=lnx(x>0)的一条切线,则实数b=( )
| A. | ln2+1 | B. | ln2-1 | C. | ln3+1 | D. | ln3-1 |
3.若△ABC的三个内角A、B、C成等差数列,则必有( )
| A. | B>60° | B. | B=60° | C. | B<60° | D. | B≠60° |
20.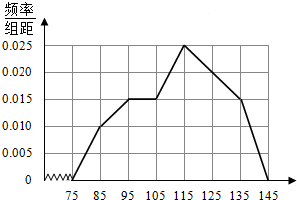 某同学将全班某次数学考试成绩整理成频率分布直方图后,并将每个小矩形上方线段的中点连接起来得到频率分布折线图(如图所示),据此估计此次考试成绩的众数是( )
某同学将全班某次数学考试成绩整理成频率分布直方图后,并将每个小矩形上方线段的中点连接起来得到频率分布折线图(如图所示),据此估计此次考试成绩的众数是( )
 某同学将全班某次数学考试成绩整理成频率分布直方图后,并将每个小矩形上方线段的中点连接起来得到频率分布折线图(如图所示),据此估计此次考试成绩的众数是( )
某同学将全班某次数学考试成绩整理成频率分布直方图后,并将每个小矩形上方线段的中点连接起来得到频率分布折线图(如图所示),据此估计此次考试成绩的众数是( )| A. | 100 | B. | 110 | C. | 115 | D. | 120 |
17.设P是△ABC所在平面内的一点,$\overrightarrow{BA}$+$\overrightarrow{BC}$=$\overrightarrow{BQ}$,其中P是线段BQ的中点,则( )
| A. | $\overrightarrow{PA}$+$\overrightarrow{PB}$=$\overrightarrow{0}$ | B. | $\overrightarrow{PC}$+$\overrightarrow{PA}$=$\overrightarrow{0}$ | C. | $\overrightarrow{PB}$+$\overrightarrow{PC}$=$\overrightarrow{0}$ | D. | $\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$=$\overrightarrow{0}$ |
9.把三进制数1021(3)化为十进制数等于( )
| A. | 102 | B. | 34 | C. | 12 | D. | 46 |