题目内容
证明：
（1）
=
；
（2）tan3α-tan2α-tanα=tan3αtan2αtanα．
（1）
| tanα-tanβ |
| tanα+tanβ |
| sin(α-β) |
| sin(α+β) |
（2）tan3α-tan2α-tanα=tan3αtan2αtanα．
分析：（1）已知等式左边利用同角三角函数间的基本关系化简，去分母后利用两角和与差的正弦函数公式化简，得到结果与右边相等，得证；
（2）利用两角和与差的正切函数公式得到tan3α=tan（α+2α）=
，去分母整理即可得证．
（2）利用两角和与差的正切函数公式得到tan3α=tan（α+2α）=
| tanα+tan2α |
| 1-tanαtan2α |
解答：解：（1）等式左边=
=
=
=右边，
则原等式成立；
（2）∵tan3α=tan（α+2α）=
，
∴tan3α（1-tanαtan2α）=tanα+tan2α，
整理得：tan3α-tan2α-tanα=tanαtan2αtan3α．
| ||||
|
| sinαcosβ-cosαsinβ |
| sinαcosβ+cosαsinβ |
| sin(α-β) |
| sin(α+β) |
则原等式成立；
（2）∵tan3α=tan（α+2α）=
| tanα+tan2α |
| 1-tanαtan2α |
∴tan3α（1-tanαtan2α）=tanα+tan2α，
整理得：tan3α-tan2α-tanα=tanαtan2αtan3α．
点评：此题考查了二倍角的正切函数公式，同角三角牌函数间的基本关系，以及两角和与差的正切函数公式，熟练掌握公式是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
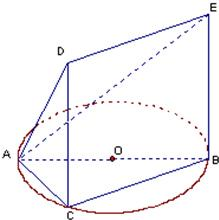如图，一简单几何体的一个面ABC内接于圆O，AB是圆O的直径，四边形DCBE为平行四边形，且DC⊥平面ABC，
如图一简单几何体的一个面ABC内接于圆O，G，H分别是AE，BC的中点，AB是圆O的直径，四边形DCBE为平行四边形，且DC⊥平面ABC．
;
＜2.