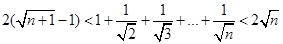题目内容
用放缩法证明下列不等式:(1)若tanθ=ntanφ(tanθ≠0,n>0),则tan2(θ-φ)≤![]() ;
;
(2)已知a>0,b>0,c>0,d>0,求证:1<![]() <2.
<2.
分析:证明不等式常常需要根据不等式的性质对原不等式的一端进行“同向”变形,即进行放大或缩小.这种利用放缩原理证明不等式的方法叫做放缩法.在放缩代换中常用下列变形:
①A>B,B>C,则A>C;②A=B,B>C,则A>C;③A>B,B=C,则A>C.
证明:(1)∵tanθ=ntanφ,且tanφ≠0,
∴tan2(θ-φ)=(![]() )2=[
)2=[![]() ]2≤
]2≤![]() .
.
故原不等式成立.
(2)∵a>0,b>0,c>0,d>0,则![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
将以上各式相加,得![]()
![]() ,
,
即1<![]() <2成立.
<2成立.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
 ,如果
,如果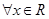 ,
, ,求
,求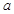 的取值范围.
的取值范围.