题目内容
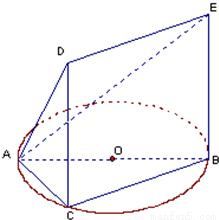
如图,一简单几何体的一个面ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,且DC⊥平面ABC,
(1)证明:平面ACD⊥平面ADE;
(2)若AB=2,BC=1,tan∠EAB=
,试求该几何体的体积V.
(1)证明:平面ACD⊥平面ADE;
(2)若AB=2,BC=1,tan∠EAB=
| ||
| 2 |


(1)证明:∵DC⊥平面ABC,BC?平面ABC,
∴DC⊥BC,
∵AB是圆O的直径,
∴BC⊥AC且DC∩AC=C,
∴BC⊥平面ADC,
∵四边形DCBE为平行四边形,
∴DE∥BC,
∴DE⊥平面ADC,
又∵DE?平面ADE,
∴平面ACD⊥平面ADE;
(2)所求简单组合体的体积:V=VE-ABC+VE-ADC
∵AB=2,BC=1,tan∠EAB=
| EB |
| AB |
| ||
| 2 |
∴BE=
| 3 |
| AB2-BC2 |
| 3 |
∴VE-ADC=
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 2 |
VE-ABC=
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 2 |
∴该简单几何体的体积V=1;

练习册系列答案
相关题目
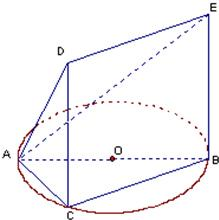 如图,一简单几何体的一个面ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,且DC⊥平面ABC,
如图,一简单几何体的一个面ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,且DC⊥平面ABC,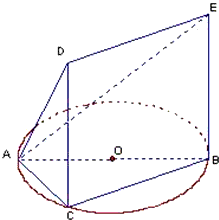 如图,一简单几何体的一个面ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,且DC⊥平面ABC,
如图,一简单几何体的一个面ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,且DC⊥平面ABC,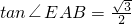 ,试求该几何体的体积V.
,试求该几何体的体积V. ,试求该几何体的体积V.
,试求该几何体的体积V.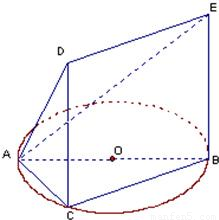
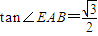 ,试求该几何体的体积V.
,试求该几何体的体积V.