题目内容
若中心在原点,焦点在坐标轴上的椭圆短轴端点是双曲线y2-x2=1的顶点,且该椭圆的离心率与此双曲线的离心率的乘积为1,则该椭圆的方程为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:根据双曲线方程求得其焦点坐标和离心率,进而可得椭圆的焦点坐标和离心率,求得椭圆的长半轴和短半轴的长,进而可得椭圆的方程.
解答:解:设椭圆方程为
+
=1,离心率为e
双曲线y2-x2=1的顶点是(0,1),所以b=1.
∵双曲线y2-x2=1的离心率为
=
∴e=
,即
=
=
=
∴a2=2
∴所求的椭圆方程为
+y2=1.
故选B.
| x2 |
| a2 |
| y2 |
| b2 |
双曲线y2-x2=1的顶点是(0,1),所以b=1.
∵双曲线y2-x2=1的离心率为
| 12+12 |
| 2 |
∴e=
| 1 | ||
|
| c |
| a |
| ||
| a |
| ||
| a |
| 1 | ||
|
∴a2=2
∴所求的椭圆方程为
| x2 |
| 2 |
故选B.
点评:本题主要考查了双曲线的性质和椭圆的标准方程.要记住双曲线和椭圆的定义和性质.

练习册系列答案
相关题目
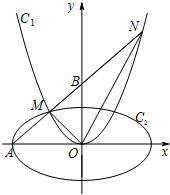 (2012•深圳二模)如图,M,N是抛物线C1:x2=4y上的两动点(M,N异于原点O),且∠OMN的角平分线垂直于y轴,直线MN与x轴,y轴分别相交于A,B.
(2012•深圳二模)如图,M,N是抛物线C1:x2=4y上的两动点(M,N异于原点O),且∠OMN的角平分线垂直于y轴,直线MN与x轴,y轴分别相交于A,B.