题目内容
(2013•蓟县二模)若中心在原点,焦点在坐标轴上的双曲线的顶点是椭圆
+y2=1短轴端点,且该双曲线的离心率与此椭圆的离心率之积为1,则该双曲线的方程为( )
| x2 |
| 2 |
分析:求出已知椭圆的短轴顶点坐标,得到双曲线的顶点为(0,±1),从而设其方程为y2-
=1(b>0),再由已知条件算出双曲线的离心率e=
,建立方程组解出b=1,从而得到所求双曲线的方程.
| x2 |
| b2 |
| 2 |
解答:解:∵椭圆
+y2=1的短轴端点坐标为(0,±1),
∴双曲线的顶点为(0,±1),可设方程为y2-
=1(b>0)
∵双曲线的离心率等于椭圆的离心率的倒数
∴由椭圆
+y2=1的离心率为
,得双曲线的离心率e=
=
解之得b=1,从而双曲线的方程为y2-x2=1
故选:B
| x2 |
| 2 |
∴双曲线的顶点为(0,±1),可设方程为y2-
| x2 |
| b2 |
∵双曲线的离心率等于椭圆的离心率的倒数
∴由椭圆
| x2 |
| 2 |
| ||
| 2 |
| ||
| 1 |
| 2 |
解之得b=1,从而双曲线的方程为y2-x2=1
故选:B
点评:本题给出双曲线的顶点是椭圆的短轴端点,在已知离心率的情况下求双曲线的方程.着重考查了椭圆、双曲线的标准方程与简单几何性质等知识,属于基础题.

练习册系列答案
相关题目
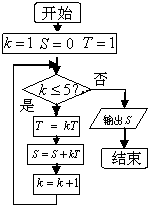 (2013•蓟县二模)如果执行如面的程序框图,那么输出的S=( )
(2013•蓟县二模)如果执行如面的程序框图,那么输出的S=( )