题目内容
已知向量
=（
，
sinx+
cosx）和向量
=（1，f（x）），且
∥
．
（1）求函数f（x）的最小正周期和最大值；
（2）已知△ABC的三个内角分别为A，B，C，若有f（A-
）=
，BC=
，sinB=
，求AC的长度．
| a |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| b |
| a |
| b |
（1）求函数f（x）的最小正周期和最大值；
（2）已知△ABC的三个内角分别为A，B，C，若有f（A-
| π |
| 3 |
| 3 |
| 7 |
| ||
| 7 |
考点：三角函数的周期性及其求法,平面向量共线（平行）的坐标表示
专题：三角函数的图像与性质,平面向量及应用
分析：（1）利用向量共线定理、两角和差的正弦公式、三角函数的性质即可得出；
（2）利用正弦定理即可得出．
（2）利用正弦定理即可得出．
解答：
解：（1）∵
∥
，∴
f(x)-(
sinx+
cosx)=0，化为f（x）=sinx+
cosx=2sin(x+
)．
∴函数f（x）的周期为2π，最大值为2．
（2）∵f(A-
)=
得2sinA=
，即sinA=
，
由正弦定理得
=
，又BC=
，sinB=
，则AC=
=2．
| a |
| b |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| π |
| 3 |
∴函数f（x）的周期为2π，最大值为2．
（2）∵f(A-
| π |
| 3 |
| 3 |
| 3 |
| ||
| 2 |
由正弦定理得
| BC |
| sinA |
| AC |
| sinB |
| 7 |
| ||
| 7 |
| BCsinB |
| sinA |
点评：本题考查了向量共线定理、两角和差的正弦公式、三角函数的性质、正弦定理，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
已知α，β∈R，设p：α＞β，设q：α-sinβcosα＞β-sinαcosβ，则p是q的（ ）
| A、充分必要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |
如图，在四棱锥S-ABCD中，底面ABCD是矩形，AD=2AB，SA=SD，SA⊥AB，N是棱AD的中点．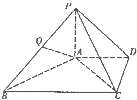
如图，在四棱锥P-ABCD中，PA⊥平面ABCD，AD∥BC，BC=2AD，PB⊥AC，Q是线段PB的中点．