题目内容
已知等差数列 的公差不为零,
的公差不为零, ,等比数列
,等比数列 的前3项满足
的前3项满足 .
.
(Ⅰ)求数列 与
与 的通项公式;
的通项公式;
(Ⅱ)设 …
… ,是否存在最大整数
,是否存在最大整数 ,使对任意的
,使对任意的 ,均有
,均有 总成立?若存在,求出
总成立?若存在,求出 的值;若不存在,请说明理由
的值;若不存在,请说明理由
(Ⅰ) ;(Ⅱ)
;(Ⅱ) .
.
【解析】
试题分析:(Ⅰ)由已知可设公差为的d,依题意可得 ,
,
联立解得: ,从而可求数列
,从而可求数列 与
与 的通项公式;
的通项公式;
(Ⅱ)依题意可得 ,假设存在整数m使
,假设存在整数m使 ,成立,即
,成立,即
记 ,则
,则 ,从而求出
,从而求出 ,即有存在最大的整数m=12,使
,即有存在最大的整数m=12,使 .
.
试题解析:(Ⅰ)由已知可设公差为 ,则有:
,则有:
 ,联立解得:
,联立解得: ,
,

(Ⅱ)数列 代入得
代入得  ,
,
故 …
…

假设存在整数 使
使 成立,即
成立,即
记 ,则
,则 ,
,
故 为单调递增,且
为单调递增,且 .
.
故存在最大的整数 ,使
,使 恒成立.
恒成立.
考点:等差数列与等比数列的综合.

练习册系列答案
相关题目
 的单调减区间是( )
的单调减区间是( ) B.
B. C.
C. D.
D.
 若
若 ,则
,则 的值为( )
的值为( ) B.
B.
 或
或 D.
D. 或
或 ,B=
,B= ,则
,则 .
. }为等差数列,若a
}为等差数列,若a +a
+a +a
+a =
= ,则
,则 的值为( )
的值为( ) B.
B. C.
C. D.
D.
 中,角
中,角 所对的边分别是
所对的边分别是 ,若
,若 ,则
,则 ,函数
,函数 的零点分别为
的零点分别为 ,函数
,函数 的零点分别为
的零点分别为 ,则
,则 的最小值为( )
的最小值为( ) B.
B. C.
C. D.
D.
 ,
, 满足条件
满足条件 则
则 的最小值为 .
的最小值为 . ,且
,且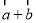 与
与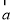 共线,那么
共线,那么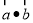 的值为( )
的值为( )