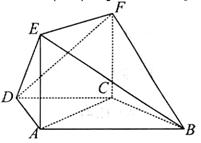
题目内容
如图,在梯形ABCD中,AB//CD,AD=DC=CB=a,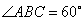 ,平面
,平面 平面ABCD,四边形ACFE是矩形,AE=a.
平面ABCD,四边形ACFE是矩形,AE=a.
(I)求证: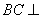 平面ACFE;
平面ACFE;
(II)求二面角B—EF—D的平面角的余弦值.
(Ⅰ)略(Ⅱ) 证明:(Ⅰ)在梯形
证明:(Ⅰ)在梯形 中,
中, ,
,
 ,
,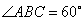
 四边形
四边形 是等腰梯形,
是等腰梯形,
且


又 平面
平面 平面
平面 ,交线为
,交线为 ,
,
 平面
平面
(Ⅱ)由(Ⅰ)知,以点 为原点,
为原点, 所在直线为
所在直线为 坐标轴,建立空间直角坐标系,则
坐标轴,建立空间直角坐标系,则

 过
过 作
作 ,
,
垂足为 . 令
. 令


由 得,
得, ,
, 即
即 

 二面角
二面角 的大小就是向量
的大小就是向量 与向量
与向量 所夹的角.
所夹的角.
 ,
,
即二面角 的平面角的余弦值为
的平面角的余弦值为 .
.
【思路点拨】(Ⅰ)证明线面垂直,一般可通线线垂直来证,而证线线垂直的过程往往通过证明直线垂直于另一条直线的平面来证明. (Ⅱ)计算二面角通过建立空间坐标系找到各点的坐标来求出二面角所在直线上向量之间的夹角来求出二面角的三角函数值.

练习册系列答案
 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案
相关题目
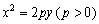 的焦点,且抛
的焦点,且抛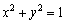 相切于点Q。
相切于点Q。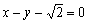 时,求抛物线C1的方程;
时,求抛物线C1的方程;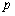 变化时,记S1 ,S2分别为△FPQ,△FOQ的面积,求
变化时,记S1 ,S2分别为△FPQ,△FOQ的面积,求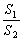 的最小值。
的最小值。 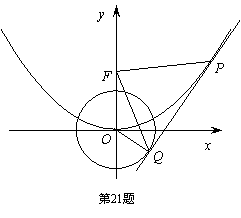
 中,内角
中,内角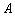 ,
,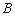 ,
,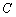 的对
的对 边分别为
边分别为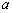 ,
, ,
,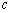 ,向量
,向量 ,
, ,且
,且 .
. ,求
,求 的面积的最大值.
的面积的最大值. 的图象大致为
的图象大致为
 中,
中, ,则
,则 ____________.
____________. ,以下说法正确的是( )
,以下说法正确的是( ) ,
, ,则
,则 ,
, ,
, ,则
,则 ,
,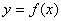 的定义域为
的定义域为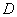 ,若对于任意
,若对于任意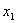 、
、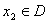 ,当
,当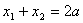 时,恒有
时,恒有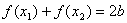 ,则称点
,则称点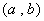 为函数
为函数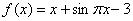 的某一个对称中心,并利用对称中心的上述定义,可得到
的某一个对称中心,并利用对称中心的上述定义,可得到 的值为……………………( )
的值为……………………( )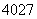 B.
B.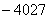 C.
C.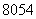 D.
D.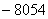
 中,记角
中,记角 、
、 、
、 所对的边分别为
所对的边分别为 、
、 、
、 ,且这三角形的三边长是公差为1的等差数列,若最小边
,且这三角形的三边长是公差为1的等差数列,若最小边 ,则
,则 ( ).
( ).







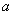 为如图所示的程序框图输出的结果,则二项式
为如图所示的程序框图输出的结果,则二项式 的展开式中常数项是
的展开式中常数项是 A. -20 B.
A. -20 B.  C. -192 D. -160
C. -192 D. -160