题目内容
有甲、乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩,得到如下所示的列联表:
|
| 优秀 | 非优秀 | 总计 |
| 甲班 | 10 | b | |
| 乙班 | c | 30 | |
| 总计 |
|
| 105 |
已知在全部105人中随机抽取1人,成绩优秀的概率为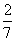 ,则下列说法正确的是( )
,则下列说法正确的是( )
参考公式:χ2=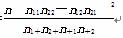
附表:
| P(χ2≥k) | 0.050[ | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
A.列联表中c的值为30,b的值为35
B.列联表中c的值为15,b的值为50
C.根据列联表中的数据,若按95%的可靠性要求,能认为“成绩与班级有关系”
D.根据列联表中的数据,若按95%的可靠性要求,不能认为“成绩与班级有关系”
C.由题意知,成绩优秀的学生数是30,成绩非优秀的学生数是75,所以c=20,b=45,选项A、B错误.根据列联表中的数据,得到χ2= ≈6.109>3.841,因此有95%的把握认为“成绩与班级有关系”,选项C正确.
≈6.109>3.841,因此有95%的把握认为“成绩与班级有关系”,选项C正确.

 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案某学校为了了解学生的日平均睡眠时间(单位:h),随机选择了n名同学进行调查.下表是这n名同学的日睡眠时间的频率分布表:
| 序号(i) | 分组(睡眠时间) | 频数(人数) | 频率 |
| 1 | [4,5) | 6 | 0.12 |
| 2 | [5,6) |
| 0.20 |
| 3 | [6,7) | a | |
| 4 | [7,8) | b | |
| 5 | [8,9) |
| 0.08 |
(1)求n的值;若a=20,将表中数据补全,并画出频率分布直方图;
(2)统计方法中,同一组数据常用该组区间的中点值(例如区间[4,5)的中点值是4.5)作为代表.若据此计算的上述数据的平均值 为6.52,求a,b的值,并由此估计该学校学生的日平均睡眠时间在7小时以上的概率.
为6.52,求a,b的值,并由此估计该学校学生的日平均睡眠时间在7小时以上的概率.
某个体服装店经营某种服装,一周内获纯利y(元)与该周每天销售这种服装的件数x之间的一组数据如下:
| x | 3[ | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 66 | 69 | 73 | 81[ | 89 | 90 | 91 |
已知: x
x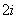 =280,
=280,
 y
y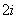 =45309,
=45309, xiyi=3487,此时r0.05=0.754.
xiyi=3487,此时r0.05=0.754.
(1)求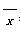 ,
,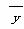 ;
;
(2)判断纯利润y与每天销售件数x之间是否线性相关.

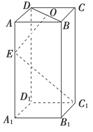
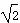 ,OE⊥EC1,求AA1的长
,OE⊥EC1,求AA1的长 .
.
 高三年级的学生人数之比为3∶3∶4,现用分层抽样的方法从该校高中三个年级的学生中抽取容量为50的样本,则应从高二年
高三年级的学生人数之比为3∶3∶4,现用分层抽样的方法从该校高中三个年级的学生中抽取容量为50的样本,则应从高二年 级抽取________名学生.
级抽取________名学生.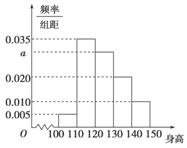
 C.x+3y-7=0 D.3x+y-5=0
C.x+3y-7=0 D.3x+y-5=0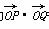 =-2,求实数k的值;
=-2,求实数k的值;