题目内容
已知数列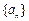 中,
中,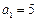 ,
, (
(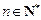 且
且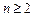 ).
).
(Ⅰ)若数列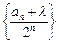 为等差数列,求实数
为等差数列,求实数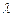 的值;
的值;
(Ⅱ)求数列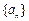 的前
的前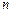 项和
项和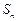 .
.
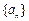 中,
中,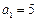 ,
, (
(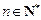 且
且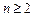 ).
).(Ⅰ)若数列
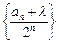 为等差数列,求实数
为等差数列,求实数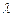 的值;
的值;(Ⅱ)求数列
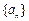 的前
的前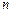 项和
项和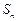 .
.(1) (2)
(2)
 (2)
(2)
(Ⅰ)因为 (
(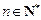 且
且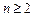 ),所以
),所以
 .
.
显然,当且仅当 ,即
,即 时,数列
时,数列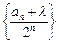 为等差数列;
为等差数列;
(Ⅱ)由(Ⅰ)的结论知:数列 是首项为
是首项为 ,公差为1的等差数列,
,公差为1的等差数列,
故有 ,即
,即 (
(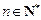 ).
).
因此,有 ,
,
 ,
,
两式相减,得 , 整理,得
, 整理,得 (
(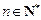 ).
).
 (
(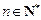 且
且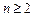 ),所以
),所以 .
.显然,当且仅当
 ,即
,即 时,数列
时,数列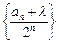 为等差数列;
为等差数列;(Ⅱ)由(Ⅰ)的结论知:数列
 是首项为
是首项为 ,公差为1的等差数列,
,公差为1的等差数列,故有
 ,即
,即 (
(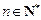 ).
).因此,有
 ,
, ,
,两式相减,得
 , 整理,得
, 整理,得 (
(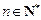 ).
).
练习册系列答案
相关题目
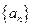 中,
中,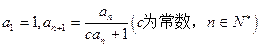 ,且
,且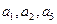 成公比不等于1的等比数列
成公比不等于1的等比数列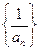 是等差数列; (2)求c的值;
是等差数列; (2)求c的值;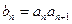 ,数列
,数列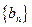 的前
的前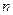 项和为
项和为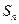 ,求
,求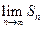
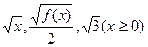 成等差数列.又数列
成等差数列.又数列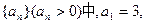 此数列的前n项的和Sn(
此数列的前n项的和Sn(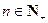 )对所有大于1的正整数n都有
)对所有大于1的正整数n都有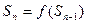 .(1)求数列
.(1)求数列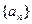 的第n+1项;(2)若
的第n+1项;(2)若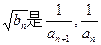 的等比中项,且Tn为{bn}的前n项和,求Tn.
的等比中项,且Tn为{bn}的前n项和,求Tn. 中,已知
中,已知 .
. 且
且 的前项
的前项 和为
和为 ,求证:
,求证: .
.


 成等差数列,且
成等差数列,且 成等比数列,则
成等比数列,则 _ 。
_ 。