题目内容
在数列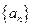 中,
中,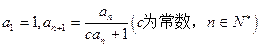 ,且
,且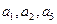 成公比不等于1的等比数列
成公比不等于1的等比数列
(1)求证:数列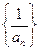 是等差数列; (2)求c的值;
是等差数列; (2)求c的值;
(3)设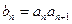 ,数列
,数列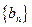 的前
的前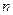 项和为
项和为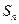 ,求
,求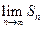
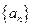 中,
中,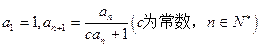 ,且
,且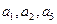 成公比不等于1的等比数列
成公比不等于1的等比数列(1)求证:数列
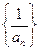 是等差数列; (2)求c的值;
是等差数列; (2)求c的值;(3)设
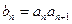 ,数列
,数列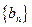 的前
的前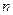 项和为
项和为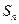 ,求
,求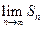
⑴ 由 可得
可得 即
即 ,
, .所以数列
.所以数列 为等差数列;
为等差数列;
⑵设数列 的公差为
的公差为 ,则
,则 ,即
,即 ,
,
因为 成等比数列,故
成等比数列,故 ,即
,即 ,解之可得
,解之可得 或2,
或2,
因为 成公比不为1的等比数列,所以
成公比不为1的等比数列,所以 ,
, ,
,
又 ,所以
,所以 .
.
⑶由⑵知 ,则
,则

所以
 可得
可得 即
即 ,
, .所以数列
.所以数列 为等差数列;
为等差数列;⑵设数列
 的公差为
的公差为 ,则
,则 ,即
,即 ,
,因为
 成等比数列,故
成等比数列,故 ,即
,即 ,解之可得
,解之可得 或2,
或2,因为
 成公比不为1的等比数列,所以
成公比不为1的等比数列,所以 ,
, ,
,又
 ,所以
,所以 .
.⑶由⑵知
 ,则
,则

所以

⑴对递推式 进行变形可以证明数列
进行变形可以证明数列 为等差数列;⑵因为
为等差数列;⑵因为 成等比数列,结合⑴可求出参数c的值;⑶由前两问可以求出数列
成等比数列,结合⑴可求出参数c的值;⑶由前两问可以求出数列 的通项公式,因为
的通项公式,因为 从而求出
从而求出 .
.
 进行变形可以证明数列
进行变形可以证明数列 为等差数列;⑵因为
为等差数列;⑵因为 成等比数列,结合⑴可求出参数c的值;⑶由前两问可以求出数列
成等比数列,结合⑴可求出参数c的值;⑶由前两问可以求出数列 的通项公式,因为
的通项公式,因为 从而求出
从而求出 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
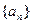 的前n项和为Sn,点
的前n项和为Sn,点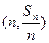 的直线
的直线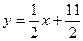 上,数列
上,数列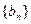 满足
满足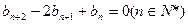 ,
,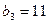 ,且
,且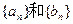 的通项公式;(Ⅱ)设
的通项公式;(Ⅱ)设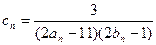 ,记数列
,记数列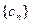 的前n项和为Tn,求使不等式
的前n项和为Tn,求使不等式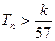 对一切
对一切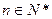 都成立的最大正整数k的值.
都成立的最大正整数k的值.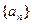 是正项等差数列,若
是正项等差数列,若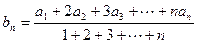 ,则数列
,则数列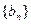 也为等差数列,类比上述结论,写出正项等比数列
也为等差数列,类比上述结论,写出正项等比数列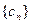 ,若
,若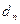 = ,则数列
= ,则数列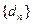 也为等比数列。
也为等比数列。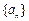 中,
中,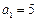 ,
, (
(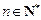 且
且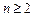 ).
).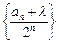 为等差数列,求实数
为等差数列,求实数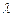 的值;
的值;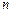 项和
项和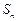 .
.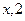 ),b =(
),b =(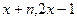 )(
)(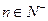 ),函数
),函数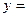 a·b在[0,1]上的最小值与最大值的和为
a·b在[0,1]上的最小值与最大值的和为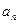 ,又数列{
,又数列{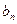 }满足:
}满足: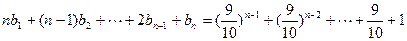 .
.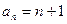 ;
;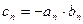 ,试问数列{
,试问数列{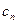 }中,是否存在正整数
}中,是否存在正整数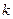 ,使得对于任意的正整数
,使得对于任意的正整数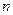 ,都有
,都有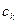 成立?证明你的结论.
成立?证明你的结论.
 小题满分14分)已知
小题满分14分)已知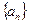 是正数组成的数列,
是正数组成的数列,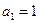 ,且点(
,且点(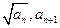 )(n
)(n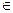 N*)在
N*)在 函数
函数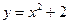 的图象上.(Ⅰ)求数列
的图象上.(Ⅰ)求数列 (Ⅱ)若
(Ⅱ)若
 数列
数列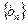
 满足
满足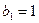 ,
,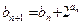 ,求数列
,求数列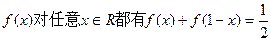 (I)求
(I)求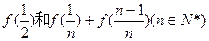 的值;(II)数列{an}满足
的值;(II)数列{an}满足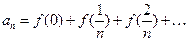
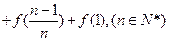 数列{an}是等差数列吗?请给予证明;
数列{an}是等差数列吗?请给予证明;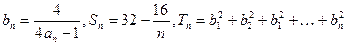 ,试比较Tn与Sn的大小.
,试比较Tn与Sn的大小.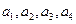 成等差数列,且
成等差数列,且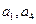 为方程方程
为方程方程 的两根,则
的两根,则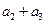 等于 。
等于 。