题目内容
数列{an}的前n项和为Sn,a1=2,an+1=3Sn
(1)求数列{an}的通项公式;
(2)令bn=
,求数列{bn}的前n项和Tn.
(1)求数列{an}的通项公式;
(2)令bn=
|
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)由已知条件推导出数列{an}(n≥2,n∈Z)是以4为公比的等比数列,由此能求出an=
.
(2)由bn=
,知当n=2k+1,k∈N*时,Tn=[1+3+5+…+(2k+1)]+(a2+a4+a6+…+a2k)
=(k+1)2+(6+6•42+6•44+…+6•42k-2);当n=2k,k∈N*时,Tn=[1+3+5+…+(2k-1)]+(a2+a4+a6+…+a2k)=
+(6+6•42+6•44+…+6•42k-2),由此能求出结果.
|
(2)由bn=
|
=(k+1)2+(6+6•42+6•44+…+6•42k-2);当n=2k,k∈N*时,Tn=[1+3+5+…+(2k-1)]+(a2+a4+a6+…+a2k)=
| k(1+2k-1) |
| 2 |
解答:
解:(1)数列{an}的前n项和为Sn,a1=2,an+1=3Sn,
由an+1=3Sn①,
得an+2=3Sn+1②,
②-①得:an+2-an+1=3an+1
∴
=4
∴数列{an}(n≥2,n∈Z)是以4为公比的等比数列
其中,a2=3S1=3a1=6
∴an=
.
(2)∵bn=
,
∴当n=2k+1,k∈N*时,
Tn=[1+3+5+…+(2k+1)]+(a2+a4+a6+…+a2k)
=(k+1)2+(6+6•42+6•44+…+6•42k-2)
=(k+1)2+
=
+
=
-
(1-4n-1).
当n=2k,k∈N*时,
Tn=[1+3+5+…+(2k-1)]+(a2+a4+a6+…+a2k)
=
+(6+6•42+6•44+…+6•42k-2)
=k2+
=
-
(1-4n).
∴Tn=
.
由an+1=3Sn①,
得an+2=3Sn+1②,
②-①得:an+2-an+1=3an+1
∴
| an+2 |
| an+1 |
∴数列{an}(n≥2,n∈Z)是以4为公比的等比数列
其中,a2=3S1=3a1=6
∴an=
|
(2)∵bn=
|
∴当n=2k+1,k∈N*时,
Tn=[1+3+5+…+(2k+1)]+(a2+a4+a6+…+a2k)
=(k+1)2+(6+6•42+6•44+…+6•42k-2)
=(k+1)2+
| 6(1-16k) |
| 1-16 |
=
| (n+1)2 |
| 4 |
6(1-16
| ||
| 1-16 |
=
| (n+1)2 |
| 4 |
| 2 |
| 5 |
当n=2k,k∈N*时,
Tn=[1+3+5+…+(2k-1)]+(a2+a4+a6+…+a2k)
=
| k(1+2k-1) |
| 2 |
=k2+
| 6(1-16k) |
| 1-16 |
=
| n2 |
| 4 |
| 2 |
| 5 |
∴Tn=
|
点评:本题考查数列的通项公式的求法,考查数列的前m项和的求法,解题时要认真审题,注意分类讨论思想的合理运用.

练习册系列答案
相关题目
 华罗庚中学高二排球队和篮球队各有10名同学,现测得排球队10人的身高(单位:cm)分别是:162、170、171、182、163、158、179、168、183、168,篮球队10人的身高(单位:cm)分别是:170、159、162、173、181、165、176、168、178、179.
华罗庚中学高二排球队和篮球队各有10名同学,现测得排球队10人的身高(单位:cm)分别是:162、170、171、182、163、158、179、168、183、168,篮球队10人的身高(单位:cm)分别是:170、159、162、173、181、165、176、168、178、179.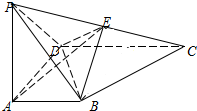 如图,在四棱锥P-ABCD中,AD=CD=2AB=2,PA⊥AD,AB∥CD,CD⊥AD,E为PC的中点,且DE=EC.
如图,在四棱锥P-ABCD中,AD=CD=2AB=2,PA⊥AD,AB∥CD,CD⊥AD,E为PC的中点,且DE=EC. 函数f(x)=Asin(wx+ϕ),(A,w,ϕ是常数,A>0,w>0,|ϕ|<
函数f(x)=Asin(wx+ϕ),(A,w,ϕ是常数,A>0,w>0,|ϕ|<