题目内容
若球的大圆的面积扩大为原来的3倍,则它的体积扩大为原来的 ( )
| A.3倍 | B.27倍 | C.3 倍 倍 | D.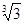 倍 倍 |
C
分析:直接应用公式化简可得球的半径扩大的倍数,然后求出体积扩大的倍数.
解:设原球的半径R
∵球的大圆的面积扩大为原来的3倍,
则半径扩大
 倍,
倍,∴体积扩大3
 倍
倍故选C.

练习册系列答案
相关题目
题目内容
| A.3倍 | B.27倍 | C.3 倍 倍 | D.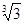 倍 倍 |
 倍,
倍, 倍
倍