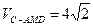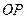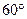题目内容
(本小题满分12分)
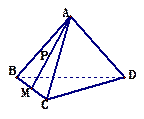
如图所示,在正三棱柱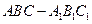 中,底面边长为
中,底面边长为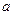 ,侧棱长为
,侧棱长为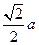 ,
,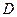 是棱
是棱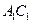 的中点.
的中点.
(Ⅰ)求证: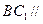 平面
平面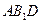 ;(Ⅱ)求二面角
;(Ⅱ)求二面角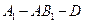 的大小;
的大小;
(Ⅲ)求点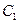 到平面
到平面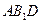 的距离.
的距离.
如图所示,在正三棱柱
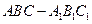 中,底面边长为
中,底面边长为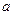 ,侧棱长为
,侧棱长为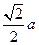 ,
,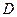 是棱
是棱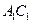 的中点.
的中点.
|
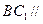 平面
平面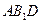 ;(Ⅱ)求二面角
;(Ⅱ)求二面角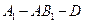 的大小;
的大小;(Ⅲ)求点
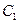 到平面
到平面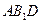 的距离.
的距离.解:(Ⅰ) 连结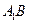 与
与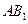 交于
交于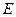 ,
,
则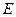 为
为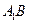 的中点,
的中点,
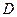 为
为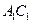 的中点,
的中点,
 为
为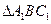 的中位线,
的中位线,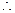
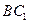 //
// . 又
. 又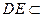 平面
平面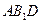 ,
,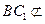 平面
平面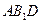
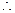
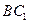 //平面
//平面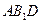 ………………4分
………………4分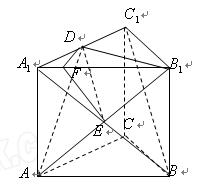
(Ⅱ)(解法1)过 作
作 于
于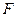 ,由正三棱柱的性质可知,
,由正三棱柱的性质可知,
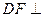 平面
平面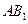 ,连结
,连结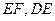 ,在正
,在正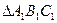 中,
中, 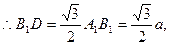
在直角三角形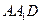 中,
中,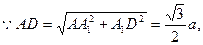
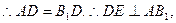
由三垂线定理的逆定理可得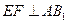 .则
.则 为二面角
为二面角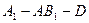 的平面角,
的平面角,
又得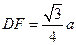 ,
,
 ,
,
∴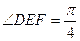 .故所求二面角
.故所求二面角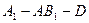 的大小为
的大小为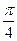 .………………8分
.………………8分
解法(2)(向量法)
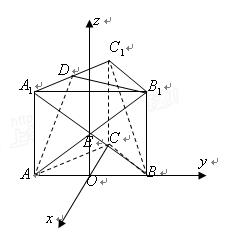
建立如图所示空间直角坐标系,则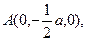
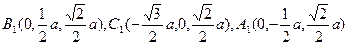

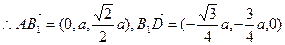 。
。
设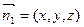 是平面
是平面 的一个法向量,则可得
的一个法向量,则可得
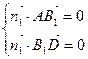 ,所以
,所以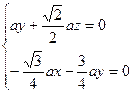 即
即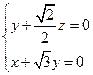 取
取
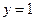 可得
可得
又平面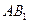 的一个法向量
的一个法向量 设
设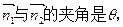 则
则
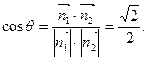 又知二面角
又知二面角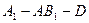 是锐角,所以二面角
是锐角,所以二面角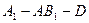 的
的 大小是
大小是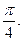 ……………………………………………………………………8分
……………………………………………………………………8分
(Ⅲ)设求点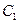 到平面
到平面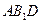 的距离
的距离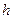 ;因
;因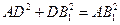 ,所以
,所以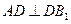 ,故
,故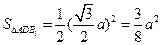 ,而
,而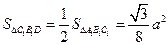 ………………10分
………………10分
由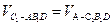
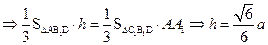 ……………12分
……………12分
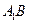 与
与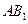 交于
交于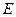 ,
,则
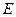 为
为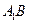 的中点,
的中点,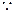
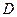 为
为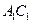 的中点,
的中点,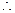
 为
为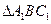 的中位线,
的中位线,
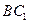 //
// . 又
. 又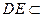 平面
平面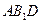 ,
,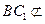 平面
平面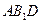
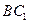 //平面
//平面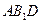 ………………4分
………………4分
(Ⅱ)(解法1)过
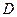 作
作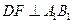 于
于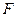 ,由正三棱柱的性质可知,
,由正三棱柱的性质可知,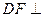 平面
平面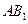 ,连结
,连结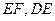 ,在正
,在正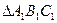 中,
中, 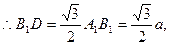
在直角三角形
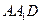 中,
中,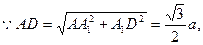
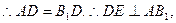
由三垂线定理的逆定理可得
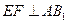 .则
.则 为二面角
为二面角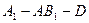 的平面角,
的平面角,又得
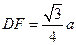 ,
, ,
,
∴
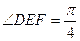 .故所求二面角
.故所求二面角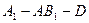 的大小为
的大小为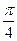 .………………8分
.………………8分解法(2)(向量法)

建立如图所示空间直角坐标系,则
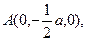
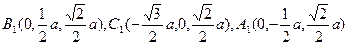

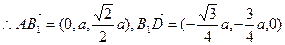 。
。设
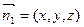 是平面
是平面 的一个法向量,则可得
的一个法向量,则可得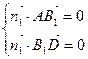 ,所以
,所以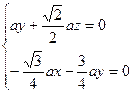 即
即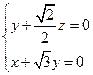 取
取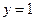 可得
可得
又平面
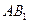 的一个法向量
的一个法向量 设
设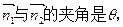 则
则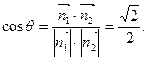 又知二面角
又知二面角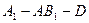 是锐角,所以二面角
是锐角,所以二面角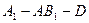 的
的 大小是
大小是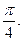 ……………………………………………………………………8分
……………………………………………………………………8分(Ⅲ)设求点
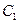 到平面
到平面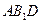 的距离
的距离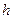 ;因
;因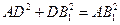 ,所以
,所以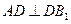 ,故
,故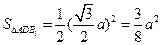 ,而
,而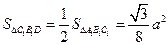 ………………10分
………………10分由
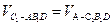
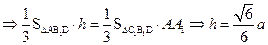 ……………12分
……………12分略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,AP=BQ=b(0<b<1),截面PQEF∥
中,AP=BQ=b(0<b<1),截面PQEF∥ ,截面PQGH∥
,截面PQGH∥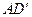 .
.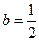 ,求
,求 与平面PQEF所成角的正弦值.
与平面PQEF所成角的正弦值.
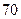 个
个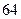 个
个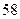 个
个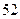 个
个 倍
倍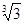 倍
倍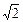 ,BC=AA'=A'C=2,∠ABC=90°,点O是点A'在底面ABCD上的射影,且点O恰好落在AC上.
,BC=AA'=A'C=2,∠ABC=90°,点O是点A'在底面ABCD上的射影,且点O恰好落在AC上.
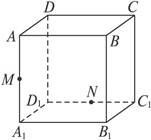
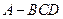 中,棱长为4,
中,棱长为4,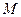 是BC的中点,
是BC的中点,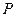 在线段
在线段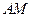 上运动(
上运动(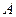 、
、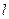
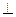 平面
平面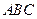 ,
,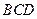 交于点Q,给出下列命题:
交于点Q,给出下列命题: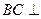 面
面
 ②Q点一定在直线DM上 ③
②Q点一定在直线DM上 ③