题目内容
(本题满分14分,第(1)小题6分,第(2)小题8分)
四棱锥P-ABCD中,PD⊥平面ABCD,PA与平面ABCD所成的角为60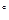 ,在四边形ABCD中,∠ADC=∠DAB=90
,在四边形ABCD中,∠ADC=∠DAB=90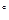 ,AB=4,CD=1,AD=2.
,AB=4,CD=1,AD=2.
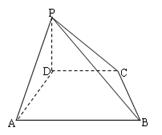
(1)求四棱锥P-ABCD的体积;
(2)求异面直线PA与BC所成的角.
四棱锥P-ABCD中,PD⊥平面ABCD,PA与平面ABCD所成的角为60
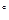 ,在四边形ABCD中,∠ADC=∠DAB=90
,在四边形ABCD中,∠ADC=∠DAB=90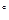 ,AB=4,CD=1,AD=2.
,AB=4,CD=1,AD=2.
(1)求四棱锥P-ABCD的体积;
(2)求异面直线PA与BC所成的角.
(1) (2)
(2)
 (2)
(2)
(1)∵PD⊥平面ABCD,
∴∠PAD为PA与平面ABCD所成的角,PD=2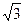 .(2分)
.(2分)
在四边形ABCD中,
∠ADC=∠DAB=90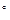 ,AB=4,CD=1,AD=2,
,AB=4,CD=1,AD=2,
∴ =5,则
=5,则 =
= =
= .(6分)
.(6分)
(2)以DA、DC、DP所在直线分别为 轴、
轴、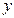 轴、
轴、 轴建立空间直角坐标系,
轴建立空间直角坐标系,
则A(2,0,0),B(2,4,0),C(0,1,0),则P(0,0,2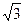 ),
),
 =(2,0,-2
=(2,0,-2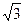 ),
),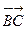 =(-2,-3,0). (10分)
=(-2,-3,0). (10分)
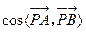 =-
=- ,即异面直线PA与BC所成的角大小为
,即异面直线PA与BC所成的角大小为 .(14分)
.(14分)
∴∠PAD为PA与平面ABCD所成的角,PD=2
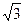 .(2分)
.(2分)在四边形ABCD中,
∠ADC=∠DAB=90
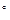 ,AB=4,CD=1,AD=2,
,AB=4,CD=1,AD=2,∴
 =5,则
=5,则 =
= =
= .(6分)
.(6分)(2)以DA、DC、DP所在直线分别为
 轴、
轴、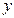 轴、
轴、 轴建立空间直角坐标系,
轴建立空间直角坐标系,则A(2,0,0),B(2,4,0),C(0,1,0),则P(0,0,2
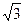 ),
), =(2,0,-2
=(2,0,-2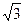 ),
),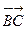 =(-2,-3,0). (10分)
=(-2,-3,0). (10分)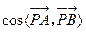 =-
=- ,即异面直线PA与BC所成的角大小为
,即异面直线PA与BC所成的角大小为 .(14分)
.(14分)
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
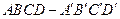 中,AP=BQ=b(0<b<1),截面PQEF∥
中,AP=BQ=b(0<b<1),截面PQEF∥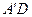 ,截面PQGH∥
,截面PQGH∥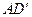 .
.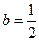 ,求
,求 与平面PQEF所成角的正弦值.
与平面PQEF所成角的正弦值.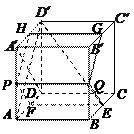


 倍
倍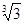 倍
倍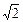 ,BC=AA'=A'C=2,∠ABC=90°,点O是点A'在底面ABCD上的射影,且点O恰好落在AC上.
,BC=AA'=A'C=2,∠ABC=90°,点O是点A'在底面ABCD上的射影,且点O恰好落在AC上.
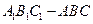 中,
中,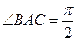 ,
,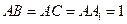 . 已知G与E分别为
. 已知G与E分别为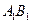 和
和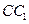 的中点,D与F分别为线段
的中点,D与F分别为线段 和
和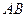 上的动点(不包括端点). 若
上的动点(不包括端点). 若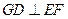 ,则线段
,则线段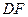 的长度的取值范围为
的长度的取值范围为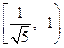



 的各顶点都在球
的各顶点都在球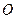 的球面上,其中
的球面上,其中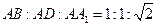 .
.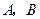 两点的球面距离记为
两点的球面距离记为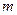 ,
,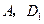 两点的球面距离记为
两点的球面距离记为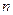 ,则
,则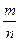 的值为 .
的值为 .