题目内容
某班40人随机分为两组,第一组18人,第二组22人,两组学生在某次数学检测中的成绩如下表: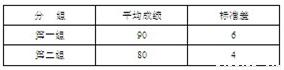
求全班的平均成绩和标准差.
【答案】分析:代入方差公式s2= [(x12+x22+…+xn2)-n
[(x12+x22+…+xn2)-n 2]即可求得方差,开根号求出标准差.
2]即可求得方差,开根号求出标准差.
解答:解:设全班的平均成绩为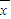 ,全班成绩的方差为s2,
,全班成绩的方差为s2,
则s12= [(x12+x22++x182)-18×902]=36,
[(x12+x22++x182)-18×902]=36,
s22= [(x192+x202++x402)-22×802]=16.
[(x192+x202++x402)-22×802]=16.
∴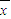 =
= (90×18+80×22)=
(90×18+80×22)=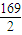 =84.5,
=84.5,
s2=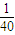 [(x12+x22++x182)+(x192+x202++x402)-40•
[(x12+x22++x182)+(x192+x202++x402)-40• 2]
2]
=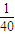 [18×(36+8100)+22×(16+6400)-40×
[18×(36+8100)+22×(16+6400)-40×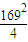 ]
]
=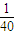 (146448+141152-10×1692)
(146448+141152-10×1692)
= ×1990=49.75.
×1990=49.75.
∴s= ≈7.05.
≈7.05.
点评:平均成绩应为总成绩除以总人数,而总成绩可由每组成绩之和求得.
 [(x12+x22+…+xn2)-n
[(x12+x22+…+xn2)-n 2]即可求得方差,开根号求出标准差.
2]即可求得方差,开根号求出标准差.解答:解:设全班的平均成绩为
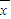 ,全班成绩的方差为s2,
,全班成绩的方差为s2,则s12=
 [(x12+x22++x182)-18×902]=36,
[(x12+x22++x182)-18×902]=36,s22=
 [(x192+x202++x402)-22×802]=16.
[(x192+x202++x402)-22×802]=16.∴
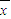 =
= (90×18+80×22)=
(90×18+80×22)=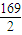 =84.5,
=84.5,s2=
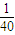 [(x12+x22++x182)+(x192+x202++x402)-40•
[(x12+x22++x182)+(x192+x202++x402)-40• 2]
2]=
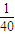 [18×(36+8100)+22×(16+6400)-40×
[18×(36+8100)+22×(16+6400)-40×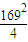 ]
]=
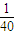 (146448+141152-10×1692)
(146448+141152-10×1692)=
 ×1990=49.75.
×1990=49.75.∴s=
 ≈7.05.
≈7.05.点评:平均成绩应为总成绩除以总人数,而总成绩可由每组成绩之和求得.

练习册系列答案
相关题目
