题目内容
有两颗正四面体的玩具,其四个面上分别标有数字 ,下面做投掷这两个正四面体玩具的试验:用(x,y)表示结果,其中x表示第1颗出现的点数(面朝下的数字),y表示第2颗出现的点数(面朝下的数字).
,下面做投掷这两个正四面体玩具的试验:用(x,y)表示结果,其中x表示第1颗出现的点数(面朝下的数字),y表示第2颗出现的点数(面朝下的数字).
(1)求事件“点数之和不小于4”的概率;
(2)求事件“点数之积能被 或
或 整除”的概率.
整除”的概率.
(1) ;(2)
;(2) .
.
【解析】
试题分析:根据题意第一颗出现的点数可以为: ,第二颗出现的点数为:
,第二颗出现的点数为: ,用列举法得到基本时间总数为
,用列举法得到基本时间总数为 个,“点数之和不小于4”包含的基本事件个数用列举法得到有个
个,“点数之和不小于4”包含的基本事件个数用列举法得到有个 ,进而得到所求事件的概率;(2)“点数之积能被
,进而得到所求事件的概率;(2)“点数之积能被 或
或 整除”的事件包含的基本事件比较多,但其对立事件只有一个
整除”的事件包含的基本事件比较多,但其对立事件只有一个 ,所以所求事件概率同过对立时间的概率得到.
,所以所求事件概率同过对立时间的概率得到.
试题解析:(1)所有的基本事件为(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4),共 个;
个;
“点数之和不小于4”包含的基本事件为(1,3),(1,4),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4)共 个,
个,
所以P(点数之和不小于4)=
(2)“点数之积能被2或3整除”的对立事件只含一个基本事件(1,1)
所以P(点数之积能被2或3整除)= .
.
考点:1.古典概型;2.对立事件的概率.

练习册系列答案
相关题目
 的前n项和为
的前n项和为 ,且4
,且4 ,2
,2 ,
, 成等差数列.若
成等差数列.若 =( )
=( ) 的单调减区间为 .
的单调减区间为 . = .
= .
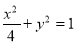 的椭圆,则由过上、下顶点和两焦点的四条直线围成图形的面积为_________.
的椭圆,则由过上、下顶点和两焦点的四条直线围成图形的面积为_________.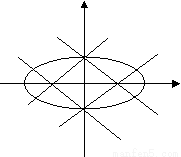
 ”的否定是_____________________.
”的否定是_____________________. 与直线
与直线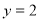 的两个相邻的交点距离等于
的两个相邻的交点距离等于 ,则
,则 的单调递增区间是( )
的单调递增区间是( )
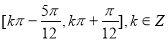

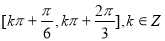
 的内角
的内角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, . 若
. 若 ,则角
,则角 _________.
_________.