题目内容
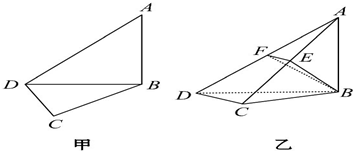
(1)如图甲,△ABC是锐角三角形,用向量方法证明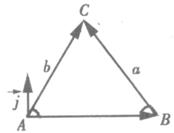
(2)如图乙,在![]() ABC中,∠A=
ABC中,∠A=![]() ,AC=2,记BC=a,试求a的取值集合M,使当a∈M时,
,AC=2,记BC=a,试求a的取值集合M,使当a∈M时,![]() ABC是唯一确定的锐角三角形.
ABC是唯一确定的锐角三角形.
(1)补充证明如下:

∵![]() +
+![]() =
=![]()
∴j·(![]() +
+![]() )=j·
)=j·![]()
∴|j|·|![]() |cos90 +|j|·|
|cos90 +|j|·|![]() |·cos(90 -B)
|·cos(90 -B)
=|j|·|![]() |cos(90 -A)
|cos(90 -A)
即asinB=bsinA 即![]()
(2)解:如图,过点C作CB1⊥AB,CB3⊥AC,CB2=AC,点B1、B2、B3均在AB上知:CB1=ACsin60 =![]() ,CB2=2,CB3=2tan60 =2
,CB2=2,CB3=2tan60 =2![]()
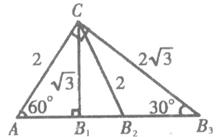
当a=![]() 或2
或2![]() 时,△ABC是Rt△
时,△ABC是Rt△
当![]() <a<2时,△ABC有两个,一个为钝角△,一个为锐角△
<a<2时,△ABC有两个,一个为钝角△,一个为锐角△
当2≤a<2![]() 时,△ABC是唯一确定的锐角△
时,△ABC是唯一确定的锐角△
当a>2![]() 时,△ABC是唯一确定的钝角△
时,△ABC是唯一确定的钝角△
综上所述,M={a|2≤a<2![]() }=[2,2
}=[2,2![]() ]
]
当a∈M时,△ABC是唯一确定的锐角△.

练习册系列答案
相关题目
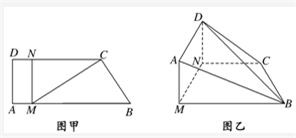 如图甲,直角梯形ABCD中,AB∥CD,∠DAB=
如图甲,直角梯形ABCD中,AB∥CD,∠DAB=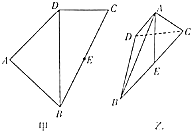 如图甲,四边形ABCD中,E是BC的中点,DB=2,DC=1,BC=
如图甲,四边形ABCD中,E是BC的中点,DB=2,DC=1,BC=