题目内容
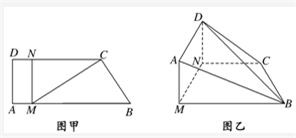 如图甲,直角梯形ABCD中,AB∥CD,∠DAB=
如图甲,直角梯形ABCD中,AB∥CD,∠DAB=| π | 2 |
(1)求证:AB∥平面DNC;
(2)当DN的长为何值时,二面角D-BC-N的大小为30°?
分析:(1)证明AB所在平面MAB与平面DNC平行,即可证明AB∥平面DNC;
(2)过N作NH⊥BC交BC延长线于H,说明∠DHN为二面角D-BC-N的平面角,利用二面角D-BC-N的大小为30°,求出DN的长.
(2)过N作NH⊥BC交BC延长线于H,说明∠DHN为二面角D-BC-N的平面角,利用二面角D-BC-N的大小为30°,求出DN的长.
解答:解:(1)证明:∵MB∥NC,MB?平面DNC,NC?平面DNC,
∴MB∥平面DNC.
同理MA∥平面DNC,又MA∩MB=M,且MA、MB?
?AB∥平面DNC.
(2)过N作NH⊥BC交BC延长线于H,

∵平面AMND⊥平面MNCB,DN⊥MN,
∴DN⊥平面MBCN,从而DH⊥BC,
∴∠DHN为二面角D-BC-N的平面角.
由MB=4,BC=2,∠MCB=90°知∠MBC=60°,
CN=4-2cos60°=3,∴NH=3sin60°=
.
由条件知:tan∠NHD=
=
,
∴DN=NH•
=
•
=
.
∴MB∥平面DNC.
同理MA∥平面DNC,又MA∩MB=M,且MA、MB?
|
(2)过N作NH⊥BC交BC延长线于H,

∵平面AMND⊥平面MNCB,DN⊥MN,
∴DN⊥平面MBCN,从而DH⊥BC,
∴∠DHN为二面角D-BC-N的平面角.
由MB=4,BC=2,∠MCB=90°知∠MBC=60°,
CN=4-2cos60°=3,∴NH=3sin60°=
3
| ||
| 2 |
由条件知:tan∠NHD=
| DN |
| NH |
| ||
| 3 |
∴DN=NH•
| ||
| 3 |
3
| ||
| 2 |
| ||
| 3 |
| 3 |
| 2 |
点评:本题考查直线与平面平行的判定,二面角及其度量,考查逻辑思维能力,空间想象能力,计算能力,是中档题.也可以通过空间直角坐标系的方法解答本题.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
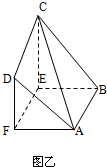
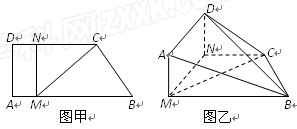
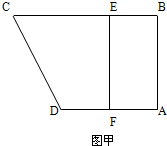 如图甲,直角梯形ABCD中,AB⊥AD,AD∥BC,F为AD的中点,E在BC上,且EF∥AB,已知AB=AD=CE=2,现沿EF把四边形CDFE折起如图乙,使平面CDFE⊥平面ABEF.
如图甲,直角梯形ABCD中,AB⊥AD,AD∥BC,F为AD的中点,E在BC上,且EF∥AB,已知AB=AD=CE=2,现沿EF把四边形CDFE折起如图乙,使平面CDFE⊥平面ABEF.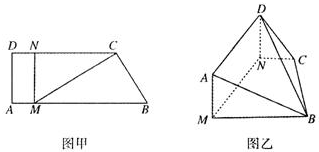 (2009•湖北模拟)如图甲,直角梯形ABCD中,AB∥CD,∠DAB=
(2009•湖北模拟)如图甲,直角梯形ABCD中,AB∥CD,∠DAB=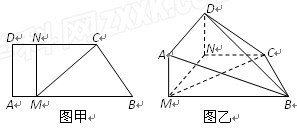
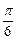 ?
?
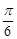 ?
?