题目内容
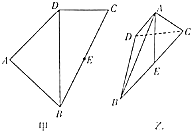 如图甲,四边形ABCD中,E是BC的中点,DB=2,DC=1,BC=
如图甲,四边形ABCD中,E是BC的中点,DB=2,DC=1,BC=| 5 |
| 2 |
(Ⅰ)求证:AE⊥平面BDC;
(Ⅱ)求点B到平面ACD的距离.
分析:(1)取BD中点M,连接AM,ME.先证明AM⊥BD,再证明BD⊥平面AEM,可得BD⊥AE,证明AE⊥ME,即可证明AE⊥平面BDC;
(2)建立空间直角坐标系,求得平面ACD的法向量,利用向量的距离公式,即可求得结论.
(2)建立空间直角坐标系,求得平面ACD的法向量,利用向量的距离公式,即可求得结论.
解答:(Ⅰ)证明:如图,取BD中点M,连接AM,ME.

∵AB=AD=
,∴AM⊥BD,
∵DB=2,DC=1,BC=
,∴DB2+DC2=BC2,∴△BCD是以BC为斜边的直角三角形,BD⊥DC,
∵E是BC的中点,∴ME为△BCD的中位线,∴ME∥
CD,
∴ME⊥BD,ME=
,…(2分)
∴∠AME是二面角A-BD-C的平面角,∴∠AME=60°.
∵AM⊥BD,ME⊥BD且AM、ME是平面AME内两条相交于点M的直线,∴BD⊥平面AEM,
∵AE?平面AEM,∴BD⊥AE.…(4分)
∵AB=AD=
,DB=2,∴△ABD为等腰直角三角形,∴AM=
BD=1,
在△AME中,由余弦定理得:AE2=AM2+ME2-2AM•ME•cos∠AME , ∴AE=
,
∴AE2+ME2=1=AM2,∴AE⊥ME,
∵BD∩ME=M,BD?平面BDC,ME?平面BDC,∴AE⊥平面BDC.…(6分)
(Ⅱ)解:如图,以M为原点,MB所在直线为x轴,ME所在直线为y轴,平行于EA的直线为z轴,建立空间直角坐标系,则由(Ⅰ)及已知条件可知B(1,0,0),E(0 ,
, 0),A(0 ,
,
),D(-1,0,0),C(-1,1,0)
,…(7分)

则
=(1 , -
, -
) ,
=(0 , -1 , 0),
=(-1 , -
, -
),
设平面ACD的法向量为
=(x,y,z),
则
∴
令x=
,则z=-2,∴
=(
, 0 , -2),…(10分)
记点B到平面ACD的距离为d,则d=|
|=|
|=
.…(12分)

∵AB=AD=
| 2 |
∵DB=2,DC=1,BC=
| 5 |
∵E是BC的中点,∴ME为△BCD的中位线,∴ME∥
| 1 |
| 2 |
∴ME⊥BD,ME=
| 1 |
| 2 |
∴∠AME是二面角A-BD-C的平面角,∴∠AME=60°.
∵AM⊥BD,ME⊥BD且AM、ME是平面AME内两条相交于点M的直线,∴BD⊥平面AEM,
∵AE?平面AEM,∴BD⊥AE.…(4分)
∵AB=AD=
| 2 |
| 1 |
| 2 |
在△AME中,由余弦定理得:AE2=AM2+ME2-2AM•ME•cos∠AME , ∴AE=
| ||
| 2 |
∴AE2+ME2=1=AM2,∴AE⊥ME,
∵BD∩ME=M,BD?平面BDC,ME?平面BDC,∴AE⊥平面BDC.…(6分)
(Ⅱ)解:如图,以M为原点,MB所在直线为x轴,ME所在直线为y轴,平行于EA的直线为z轴,建立空间直角坐标系,则由(Ⅰ)及已知条件可知B(1,0,0),E(0 ,
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
,…(7分)

则
| AB |
| 1 |
| 2 |
| ||
| 2 |
| CD |
| AD |
| 1 |
| 2 |
| ||
| 2 |
设平面ACD的法向量为
| n |
则
|
|
令x=
| 3 |
| n |
| 3 |
记点B到平面ACD的距离为d,则d=|
| ||||
|
|
| ||||
|
2
| ||
| 7 |
点评:本题考查直线和平面垂直的证明,考查求点到平面的距离,考查向量知识的运用,属于中档题.

练习册系列答案
相关题目
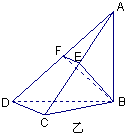
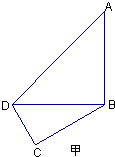 如图甲,在平面四边形ABCD中,已知∠A=45°,∠C=90°,∠ADC=105°,AB=BD,现将四边形ABCD沿BD折起,使平面ABD⊥平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.
如图甲,在平面四边形ABCD中,已知∠A=45°,∠C=90°,∠ADC=105°,AB=BD,现将四边形ABCD沿BD折起,使平面ABD⊥平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.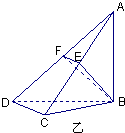
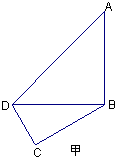 如图甲,在平面四边形ABCD中,已知∠A=45°,∠C=90°,∠ADC=105°,AB=BD,现将四边形ABCD沿BD折起,使平面ABD⊥平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.
如图甲,在平面四边形ABCD中,已知∠A=45°,∠C=90°,∠ADC=105°,AB=BD,现将四边形ABCD沿BD折起,使平面ABD⊥平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.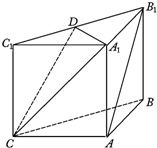 如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1,ACC1A1均为正方形,∠BAC=90°,点D是棱B1C1的中点.
如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1,ACC1A1均为正方形,∠BAC=90°,点D是棱B1C1的中点.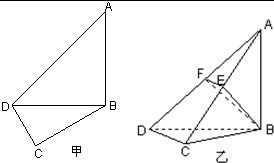 在平面四边形ABCD中,已知∠A=45°,∠C=90°,∠ADC=105°,AB=BD,现将四边形ABCD沿BD折起,使平面ABD⊥平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.
在平面四边形ABCD中,已知∠A=45°,∠C=90°,∠ADC=105°,AB=BD,现将四边形ABCD沿BD折起,使平面ABD⊥平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.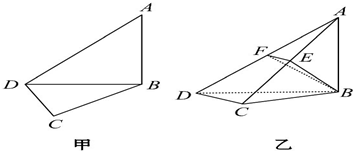
 如图甲,在平面四边形ABCD中,已知∠A=45°,∠C=90°,AB=BD=2CD,现将四边形ABCD沿BD折起,使平面ABD⊥平面BDC(如图乙),设点E为棱AD的中点.
如图甲,在平面四边形ABCD中,已知∠A=45°,∠C=90°,AB=BD=2CD,现将四边形ABCD沿BD折起,使平面ABD⊥平面BDC(如图乙),设点E为棱AD的中点.