题目内容
已知数列 的通项
的通项 ,
, .
.
(Ⅰ)求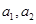 ;
;
(Ⅱ)判断数列 的增减性,并说明理由;
的增减性,并说明理由;
(Ⅲ)设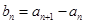 ,求数列
,求数列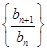 的最大项和最小项.
的最大项和最小项.
(Ⅰ) ,
, (Ⅱ)
(Ⅱ) 时,数列
时,数列 为递增数列,
为递增数列, 时,数列
时,数列 为递减数列;(Ⅲ)最大项为
为递减数列;(Ⅲ)最大项为 ,最小项为
,最小项为 。
。
解析试题分析:(Ⅰ) 直接代入即可求值(Ⅱ)用后一项减前一项,结果和0作比较。结果等于0,说明是常数列;结果大于0,说明是递增数列;结果小于0说明是递减数列。注意讨论。(Ⅱ)先求数列数列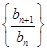 的通项公式,再用作差法判断数列的增减性,再求其最值。
的通项公式,再用作差法判断数列的增减性,再求其最值。
试题解析:(Ⅰ) ,
, . .2分
. .2分
(Ⅱ)

 .
.
则当 时,
时, ,则
,则 时,数列
时,数列 为递增数列,
为递增数列, ;
;
当 时,
时, ,数列
,数列 为递减数列,
为递减数列, . .7分
. .7分
(Ⅲ)由上问可得, ,
, .
.
令 ,即求数列
,即求数列 的最大项和最小项.
的最大项和最小项.
则

 .
.
则数列 在
在 时递减,此时
时递减,此时 ,即
,即 ;
;
数列 在
在 时递减,此时
时递减,此时 ,即
,即 .
.
因此数列 的最大项为
的最大项为 ,最小项为
,最小项为 . . .13分
. . .13分
考点:作差法比较大小,考查分类讨论思想。

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
 满足
满足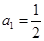 ,
, .
. 的值,由此猜测
的值,由此猜测 .
.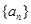 的前
的前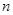 项和为
项和为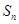 ,
,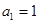 ,且
,且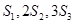 成等差数列.
成等差数列. ,求数列
,求数列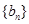 的前
的前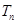 .
. 前n项和
前n项和 =
= (
(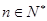 ), 数列
), 数列 为等比数列,首项
为等比数列,首项 =2,公比为q(q>0)且满足
=2,公比为q(q>0)且满足 ,
, ,
, 为等比数列.
为等比数列. ,记数列
,记数列 元的前提下,可卖出
元的前提下,可卖出 件;若做广告宣传,广告费为
件;若做广告宣传,广告费为 千元比广告费为
千元比广告费为 千元时多卖出
千元时多卖出 件.
件.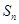 与
与 时,厂家应生产多少件这种产品,做几千元的广告,才能获利最大?
时,厂家应生产多少件这种产品,做几千元的广告,才能获利最大? 满足
满足 ,则称数列
,则称数列 中,
中, ,点
,点 在函数
在函数 的图象上,其中
的图象上,其中 为正整数.
为正整数. 是“平方递推数列”,且数列
是“平方递推数列”,且数列 为等比数列;
为等比数列; 项积为
项积为 ,即
,即 ,求
,求 ;
; ,求数列
,求数列 的前
的前 ,并求使
,并求使 的
的 ,
, ,
, .
. 为等比数列;
为等比数列; 、
、 、
、 ,使
,使 、
、 、
、 成等比数列?如果存在,求出所有符合条件的
成等比数列?如果存在,求出所有符合条件的 为等差数列,且
为等差数列,且 .
. 项和
项和 ;
; 满足
满足 求数列
求数列 是正数组成的数列,
是正数组成的数列, .若点
.若点 在函数
在函数 的导函数
的导函数 图像上.
图像上. ,是否存在最小的正数
,是否存在最小的正数 ,使得对任意
,使得对任意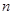
 都有
都有 成立?请说明理由.
成立?请说明理由.