题目内容
已知公比不为1的等比数列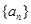 的前
的前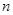 项和为
项和为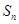 ,
,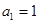 ,且
,且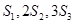 成等差数列.
成等差数列.
(1)求数列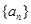 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列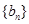 的前
的前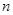 项和
项和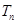 .
.
(1)数列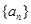 的通项公式为
的通项公式为 ; (2)
; (2) .
.
解析试题分析:(1)因为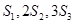 成等差数列,∴
成等差数列,∴ ,得
,得 ,则
,则 .
.
(2)先由裂项相消法求出 ,然后可直接求出数列
,然后可直接求出数列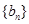 的前
的前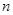 项和
项和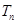 .
.
∴
试题解析:(1)∵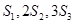 成等差数列,∴
成等差数列,∴ ,∴
,∴ ,
,
得 ,则
,则 6分
6分
(2)∵
∴ 12分
12分
考点:数列通项公式及前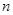 项和的求法、数列综合应用.
项和的求法、数列综合应用.

练习册系列答案
 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
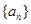 的前n项和
的前n项和 满足
满足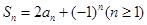
 、
、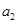 、
、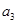 ;
;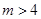 有
有
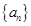 的前三项分别为
的前三项分别为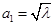 ,
, ,
,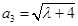 ,(其中
,(其中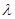 为正常数)。设
为正常数)。设
 。
。 的值;
的值;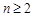 时,
时,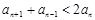 .
.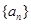 中,
中,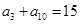 ,且
,且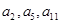 成等比数列.
成等比数列.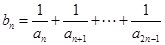 ,证明:
,证明: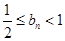 .
.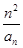 ,证明:bn≤
,证明:bn≤ .
.
 的通项
的通项 ,
, .
.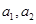 ;
;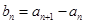 ,求数列
,求数列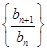 的最大项和最小项.
的最大项和最小项.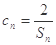 ,数列{cn}的前n项和为Tn,求证
,数列{cn}的前n项和为Tn,求证