题目内容
某产品具有一定的时效性,在这个时效期内,由市场调查可知,在不做广告宣传且每件获利 元的前提下,可卖出
元的前提下,可卖出 件;若做广告宣传,广告费为
件;若做广告宣传,广告费为 千元比广告费为
千元比广告费为 千元时多卖出
千元时多卖出 件.
件.
(Ⅰ)试写出销售量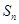 与
与 的函数关系式;
的函数关系式;
(Ⅱ)当 时,厂家应生产多少件这种产品,做几千元的广告,才能获利最大?
时,厂家应生产多少件这种产品,做几千元的广告,才能获利最大?
(Ⅰ)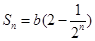 ;(Ⅱ)7875,5.
;(Ⅱ)7875,5.
解析试题分析:(Ⅰ)由条件得到 ,然后用累加法得到
,然后用累加法得到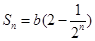 ;(Ⅱ)将
;(Ⅱ)将 代入,设获利为
代入,设获利为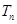 元,从而得到
元,从而得到 .然后根据不等式
.然后根据不等式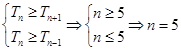 ,即做5千元的广告,再由
,即做5千元的广告,再由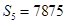 知厂家应生产7875件这种产品.
知厂家应生产7875件这种产品.
试题解析:(Ⅰ)设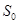 表示广告费为
表示广告费为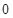 元时的销售量,
元时的销售量,
由题意知 ,
,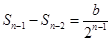 , ,
, ,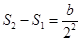 ,
,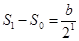 ,
,
将上述各式相加得: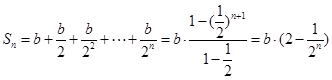 为所求.
为所求.
(Ⅱ)当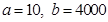 时,设获利为
时,设获利为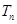 元,
元,
由题意知 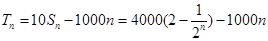 ;
;
欲使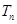 最大,则
最大,则 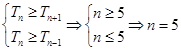 ,此时
,此时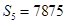 .
.
即厂家应生产7875件这种产品,做5千元的广告,才能获利最大.
考点:1.累加法求数列通项;2.数列的最大项求法.

练习册系列答案
相关题目
 ,且
,且 按某种顺序排列成等差数列.
按某种顺序排列成等差数列. 的值;
的值; 的首项和公差都为
的首项和公差都为 的首项和公比都为
的首项和公比都为 项和分别为
项和分别为 ,且
,且 ,求满足条件的自然数
,求满足条件的自然数
 的通项
的通项 ,
, .
.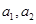 ;
;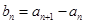 ,求数列
,求数列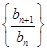 的最大项和最小项.
的最大项和最小项.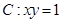 ,过
,过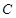 上一点
上一点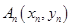 作一斜率为
作一斜率为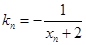 的直线交曲线
的直线交曲线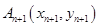 (
(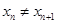 且
且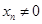 ,点列
,点列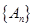 的横坐标构成数列
的横坐标构成数列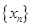 ,其中
,其中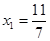 .
.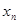 与
与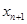 的关系式;
的关系式;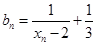 ,求证:数列
,求证:数列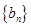 是等比数列;
是等比数列;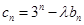 (
( 为非零整数,
为非零整数,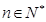 ),试确定
),试确定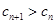 成立.
成立. 的前
的前 项和为
项和为 ,满足:
,满足:
 .递增的等比数列
.递增的等比数列 前
前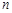 项和为
项和为 ,满足:
,满足: .
. 对
对 ,均有
,均有 成立,求
成立,求 .
.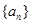 的各项均为正数,
的各项均为正数,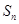 为其前
为其前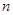 项和,对于任意的
项和,对于任意的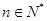 ,满足关系式
,满足关系式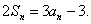
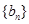 的通项公式是
的通项公式是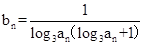 ,前
,前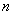 项和为
项和为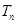 ,求证:对于任意的正整数
,求证:对于任意的正整数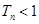 .
.