Question

【题目】选修4—4：坐标系与参数方程

在直角坐标系xOy中，设倾斜角为α的直线l：（t为参数）与曲线C：（θ为参数）相交于不同的两点A，B．

（Ⅰ）若α＝，求线段AB中点M的坐标；

（Ⅱ）若｜PA｜·｜PB｜＝｜OP｜，其中P（2，），求直线l的斜率．

Answer 1

【答案】（1）；（2）.

【解析】

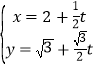试题分析：（1）将曲线的参数方程化为普通方程，当时，设点对应参数为．直线方程为代入曲线的普通方程，得，由韦达定理和中点坐标公式求得，代入直线的参数方程可得点的坐标；（2）把直线的参数方程代入椭圆的普通方程可得关于参数的一元二次方程，由已知条件和韦达定理可得，求得的值即得斜率.

试题解析：设直线上的点，对应参数分别为，．将曲线的参数方程化为普通方程．

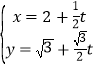（1）当时，设点对应参数为．直线方程为（为参数）．

代入曲线的普通方程，得，则，

所以，点的坐标为．

（2）将代入，得，

因为，，所以．

得．由于，故．

所以直线的斜率为．