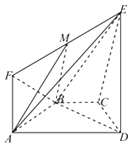
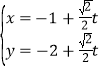题目内容
【题目】已知圆![]()
(1)求圆![]() 关于直线
关于直线![]() 对称的圆
对称的圆![]() 的标准方程;
的标准方程;
(2)过点![]() 的直线
的直线![]() 被圆
被圆![]() 截得的弦长为8,求直线
截得的弦长为8,求直线![]() 的方程;
的方程;
(3)当![]() 取何值时,直线
取何值时,直线![]() 与圆
与圆![]() 相交的弦长最短,并求出最短弦长.
相交的弦长最短,并求出最短弦长.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]()
【解析】
(1)设![]() ,根据圆心
,根据圆心![]() 与
与![]() 关于直线对称,列出方程组,求得
关于直线对称,列出方程组,求得![]() 的值,即可求解;
的值,即可求解;
(2)由圆的弦长公式,求得![]() ,根据斜率分类讨论,求得直线的斜率,即可求解;
,根据斜率分类讨论,求得直线的斜率,即可求解;
(3)由直线![]() ,得直线
,得直线![]() 过定点
过定点![]() ,根据
,根据![]() 时,弦长最短,即可求解.
时,弦长最短,即可求解.
(1)由题意,圆![]() 的圆心
的圆心![]() ,半径为
,半径为![]() ,
,
设![]() ,因为圆心
,因为圆心![]() 与
与![]() 关于直线对称,
关于直线对称,
所以 ,解得
,解得![]() ,则
,则![]() ,半径
,半径![]() ,
,
所以圆![]() 标准方程为:
标准方程为:![]()
(2)设点![]() 到直线
到直线![]() 距离为
距离为![]() ,圆的弦长公式,得
,圆的弦长公式,得![]() ,解得
,解得![]() ,
,
①当![]() 斜率不存在时,直线方程为
斜率不存在时,直线方程为![]() ,满足题意
,满足题意
②当![]() 斜率存在时,设直线方程为
斜率存在时,设直线方程为![]() ,则
,则![]() ,解得
,解得![]() ,
,
所以直线的方程为![]() ,
,
综上,直线方程为![]() 或
或![]()
(3)由直线![]() ,可化为
,可化为![]() ,可得直线
,可得直线![]() 过定点
过定点![]() ,
,
当![]() 时,弦长最短,又由
时,弦长最短,又由![]() ,可得
,可得![]() ,
,
此时最短弦长为![]() .
.

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案【题目】近年来,某市为了促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的分类垃圾箱.为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1 000吨生活垃圾,数据统计如下(单位:吨):
“厨余垃圾”箱 | “可回收物”箱 | “其他垃圾”箱 | |
厨余垃圾 | 400 | 100 | 100 |
可回收物 | 30 | 240 | 30 |
其他垃圾 | 20 | 20 | 60 |
(1)试估计厨余垃圾投放正确的概率P;
(2)试估计生活垃圾投放错误的概率;
(3)假设厨余垃圾在“厨余垃圾”箱,“可回收物”箱,“其他垃圾”箱的投放量分别为a、b、c,其中a>0,a+b+c=600. 当数据a、b、c的方差s2最大时,写出a、b、c的值(结论不要求证明),并求出此时s2的值.
【题目】为选派一名学生参加全市实践活动技能竟赛,A、B两位同学在学校的学习基地现场进行加工直径为20mm的零件测试,他俩各加工的10个零件直径的相关数据如图所示(单位:mm)

A、B两位同学各加工的10个零件直径的平均数与方差列于下表;
平均数 | 方差 | |
A | 20 | 0.016 |
B | 20 | s2B |
根据测试得到的有关数据,试解答下列问题:
(Ⅰ)计算s2B,考虑平均数与方差,说明谁的成绩好些;
(Ⅱ)考虑图中折线走势情况,你认为派谁去参赛较合适?请说明你的理由.