题目内容
14.已知数列{an}的前n项和为Sn,对于任意的正整数n都有Sn=n2,且各项均为正数的等比数列{bn}中,b6=b3b4,且b3和b5的等差中项是10.(1)求数列{an},{bn}的通项公式;
(2)若cn=an•bn,求数列{cn}的前n项和Tn.
分析 (1)当n≥2时,an=Sn-Sn-1,即可得出an;等比数列{bn}中,由b6=b3b4,利用等比数列的通项公式可得b1.设公比q>0,由b3和b5的等差中项是10.可知
b3+b5=20.解得q,从而得到bn.
(2)cn=an•bn=(2n-1)•2n-1,利用“错位相减法”与等比数列的前n项和公式即可得出.
解答 解:(1)当n≥2时,an=Sn-Sn-1=n2-(n-1)2=2n-1,
经检验n=1时也成立,
∴an=2n-1;
等比数列{bn}中,∵b6=b3b4,∴${b}_{1}{q}^{5}$=${b}_{1}^{2}{q}^{2}•{q}^{3}$,解得b1=1.
设公比q>0,由b3和b5的等差中项是10.
可知b3+b5=20.
∴q2+q4=20,
解得q=2,
从而bn=2n-1.
(2)若cn=an•bn=(2n-1)•2n-1,
∴Tn=1+3×2+5×22+…+(2n-1)•2n-1,
2Tn=2+3×22+…+(2n-3)×2n-1+(2n-1)•2n,
两式相减,得-Tn=1+2(2+22+…+2n-1)-(2n-1)•2n=1+$2×\frac{2({2}^{n-1}-1)}{2-1}$-(2n-1)•2n=-3+(3-2n)•2n,
∴Tn=3+(2n-3)•2n.
点评 本题考查了“错位相减法”、等差数列与等比数列的前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
9.已知点P在曲线C:y2=4-2x2上,点A(0,-$\sqrt{2}$),则|PA|的最大值为( )
| A. | 2-$\sqrt{2}$ | B. | 2+$\sqrt{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{2}$+1 |
19.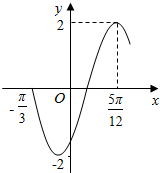 函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则这个函数的周期和初相分别是( )
函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则这个函数的周期和初相分别是( )
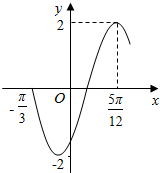 函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则这个函数的周期和初相分别是( )
函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则这个函数的周期和初相分别是( )| A. | 2,-$\frac{π}{3}$ | B. | 2,-$\frac{π}{6}$ | C. | π,-$\frac{π}{6}$ | D. | π,-$\frac{π}{3}$ |
3.已知a<b,则下列各式正确的是( )
| A. | a2<b2 | B. | ac<bc | C. | log2a<log2b | D. | 2a<2b |
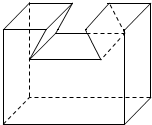 如图中的组合体的结构特征有以下几种说法:
如图中的组合体的结构特征有以下几种说法: 如图,△PBD是直角三角形,∠PDB=90°,以BA为直径作⊙O,设点C是圆⊙O与直线PD的公共点,若∠ABC=∠DBC.
如图,△PBD是直角三角形,∠PDB=90°,以BA为直径作⊙O,设点C是圆⊙O与直线PD的公共点,若∠ABC=∠DBC.