题目内容

（2012•福建）（1）选修4-2：矩阵与变换
设曲线2x2+2xy+y2=1在矩阵A=
a0
b1
（a＞0）对应的变换作用下得到的曲线为x2+y2=1．
（Ⅰ）求实数a，b的值．
（Ⅱ）求A2的逆矩阵．
分析：（Ⅰ）确定点在矩阵A=
a0
b1
（a＞0）对应的变换作用下得到点坐标之间的关系，利用变换前后的方程，即可求得矩阵A；
（Ⅱ）先计算A2的值，求出行列式的值，即可得到A2的逆矩阵．
解答：解：（Ⅰ）设曲线2x2+2xy+y2=1上的点（x，y）在矩阵A=（
a0
b1
）（a＞0）对应的变换作用下得到点（x′，y′）
则（
a0
b1
）
x
y
=
x′
y′
，∴
x′=ax
y′=bx+y

∵x′2+y′2=1
∴（ax）2+（bx+y）2=1
∴（a2+b2）x2+2bxy+y2=1
∵2x2+2xy+y2=1
∴a2+b2=2，2b=2
∴a=1，b=1
∴A=（
10
11
）
（Ⅱ）A2=（
10
11
）（
10
11
）=（
10
21
），
.
10
21
.
=1
∴A2的逆矩阵为
10
-21
点评：本题考查矩阵与变换，考查逆矩阵的求法，确定变换前后坐标之间的关系是解题的关键．
练习册系列答案
相关题目
（2012•福建模拟）双曲线
x2
a2
-
y2
b2
=1(a＞0，b＞0)的渐近线方程是2x±y=0，则其离心率为（　　）
（2012•福建）选修4-4：坐标系与参数方程
在平面直角坐标系中，以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系．已知直线l上两点M，N的极坐标分别为（2，0），（
2
3
3
，
π
2
），圆C的参数方程
x=2+2cosθ
y=-
3
+2sinθ
（θ为参数）．
（Ⅰ）设P为线段MN的中点，求直线OP的平面直角坐标方程；
（Ⅱ）判断直线l与圆C的位置关系．
（2012•福建）数列{an}的通项公式an=ncos
nπ
2
，其前n项和为Sn，则S2012等于（　　）
（2012•福建）在等差数列{an}和等比数列{bn}中，a1=b1=1，b4=8，{an}的前10项和S10=55．
（Ⅰ）求an和bn；
（Ⅱ）现分别从{an}和{bn}的前3项中各随机抽取一项，写出相应的基本事件，并求这两项的值相等的概率．
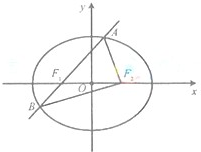（2012•福建）如图，椭圆E：
x2
a2
+
y2
b2
 =1(a＞b＞0)的左焦点为F1，右焦点为F2，离心率e=
1
2
．过F1的直线交椭圆于A、B两点，且△ABF2的周长为8．
（Ⅰ）求椭圆E的方程．
（Ⅱ）设动直线l：y=kx+m与椭圆E有且只有一个公共点P，且与直线x=4相较于点Q．试探究：在坐标平面内是否存在定点M，使得以PQ为直径的圆恒过点M？若存在，求出点M的坐标；若不存在，说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网