题目内容
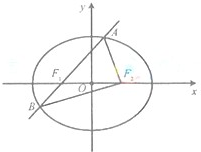 (2012•福建)如图,椭圆E:
(2012•福建)如图,椭圆E:| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
(Ⅰ)求椭圆E的方程.
(Ⅱ)设动直线l:y=kx+m与椭圆E有且只有一个公共点P,且与直线x=4相较于点Q.试探究:在坐标平面内是否存在定点M,使得以PQ为直径的圆恒过点M?若存在,求出点M的坐标;若不存在,说明理由.
分析:(Ⅰ)根据过F1的直线交椭圆于A、B两点,且△ABF2的周长为8,可得4a=8,即a=2,利用e=
,b2=a2-c2=3,即可求得椭圆E的方程.
(Ⅱ)由
,消元可得(4k2+3)x2+8kmx+4m2-12=0,利用动直线l:y=kx+m与椭圆E有且只有一个公共点P(x0,y0),可得m≠0,△=0,进而可得P(-
,
),由
得Q(4,4k+m),取k=0,m=
;k=-
,m=2,猜想满足条件的点M存在,只能是M(1,0),再进行证明即可.
| 1 |
| 2 |
(Ⅱ)由
|
| 4k |
| m |
| 3 |
| m |
|
| 3 |
| 1 |
| 2 |
解答:解:(Ⅰ)∵过F1的直线交椭圆于A、B两点,且△ABF2的周长为8.
∴4a=8,∴a=2
∵e=
,∴c=1
∴b2=a2-c2=3
∴椭圆E的方程为
+
=1.
(Ⅱ)由
,消元可得(4k2+3)x2+8kmx+4m2-12=0
∵动直线l:y=kx+m与椭圆E有且只有一个公共点P(x0,y0)
∴m≠0,△=0,∴(8km)2-4×(4k2+3)×(4m2-12)=0
∴4k2-m2+3=0①
此时x0=-
=-
,y0=
,即P(-
,
)
由
得Q(4,4k+m)
取k=0,m=
,此时P(0,
),Q(4,
),以PQ为直径的圆为(x-2)2+(y-
)2=4,交x轴于点M1(1,0)或M2(3,0)
取k=-
,m=2,此时P(1,
),Q(4,0),以PQ为直径的圆为(x-
)2+(y-
)2=
,交x轴于点M3(1,0)或M4(4,0)
故若满足条件的点M存在,只能是M(1,0),证明如下
∵
=(-
-1,
),
=(3,4k+m)
∴
•
=-
- 3+
+3=0
故以PQ为直径的圆恒过x轴上的定点M(1,0)
∴4a=8,∴a=2
∵e=
| 1 |
| 2 |
∴b2=a2-c2=3
∴椭圆E的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)由
|
∵动直线l:y=kx+m与椭圆E有且只有一个公共点P(x0,y0)
∴m≠0,△=0,∴(8km)2-4×(4k2+3)×(4m2-12)=0
∴4k2-m2+3=0①
此时x0=-
| 4km |
| 4k2+3 |
| 4k |
| m |
| 3 |
| m |
| 4k |
| m |
| 3 |
| m |
由
|
取k=0,m=
| 3 |
| 3 |
| 3 |
| 3 |
取k=-
| 1 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
| 3 |
| 4 |
| 45 |
| 16 |
故若满足条件的点M存在,只能是M(1,0),证明如下
∵
| MP |
| 4k |
| m |
| 3 |
| m |
| MQ |
∴
| MP |
| MQ |
| 12k |
| m |
| 12k |
| m |
故以PQ为直径的圆恒过x轴上的定点M(1,0)
点评:本题主要考查抛物线的定义域性质、圆的性质、直线与圆锥曲线的位置关系,考查运算能力,考查化归思想,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2012•福建)如图所示,在边长为1的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为( )
(2012•福建)如图所示,在边长为1的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为( ) (2012•福建)如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M为棱DD1上的一点.
(2012•福建)如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M为棱DD1上的一点.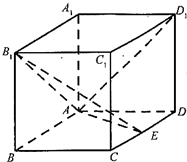 (2012•福建)如图,在长方体ABCD-A1B1C1D1中AA1=AD=1,E为CD中点.
(2012•福建)如图,在长方体ABCD-A1B1C1D1中AA1=AD=1,E为CD中点. (2012•福建)如图,等边三角形OAB的边长为
(2012•福建)如图,等边三角形OAB的边长为