题目内容
在钝角△ABC中,已知a=1,b=2,则最大边的取值范围是 .
考点:余弦定理
专题:解三角形
分析:根据三角形三边关系求出c的范围,当∠C为直角时,利用勾股定理确定c的值,故当∠C为钝角时,确定出c的范围即可.
解答:
解:根据三角形两边之和大于第三边,两边之差小于第三边,得到c的范围为1<c<3,
当∠C为直角时,c=
=
,
当∠C为钝角时,得到c>
,
当∠C为锐角时,B为钝角,此时b为最大边,1<b<3,
则最大边的范围为
<x<3.
故答案为:
<x<3
当∠C为直角时,c=
| 12+22 |
| 5 |
当∠C为钝角时,得到c>
| 5 |
当∠C为锐角时,B为钝角,此时b为最大边,1<b<3,
则最大边的范围为
| 5 |
故答案为:
| 5 |
点评:此题考查了余弦定理,以及三角形的边角关系,熟练掌握余弦定理是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知集合A={1,2,4},B={3,4,6},C={2,4},则( )
| A、A∩B=B | B、A∪B=A |
| C、A∩B⊆C | D、A⊆B |
已知f(x)=
是(-∞,+∞)上的增函数,那么a的取值范围是( )
|
A、[-
| ||
B、[
| ||
C、(
| ||
D、(
|
下列各角中与角-
终边相同的是( )
| π |
| 3 |
| A、300° | ||
| B、240° | ||
C、
| ||
D、
|
已知双曲线
-
=1(a>0,b>0)上的点(2,1)到该点较近的渐近线的距离为
(其中e为离心率),则双曲线的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| e |
A、
| ||||
B、
| ||||
| C、x2-3y2=1 | ||||
D、
|
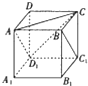 如图,正方体ABCD-A1B1C1D1,则下列五个命题:
如图,正方体ABCD-A1B1C1D1,则下列五个命题: