题目内容
已知直线y=x+m与曲线x2+y2=4交于不同的两点A,B,若|AB|≥2
,则实数m的取值范围是 .
| 3 |
考点:直线与圆相交的性质
专题:直线与圆
分析:由题意可得弦心距d=
≤1,即
≤1,由此求得m的范围.
r2-(
|
| |0-0+m| | ||
|
解答:
解:由于圆x2+y2=4的半径r=2,弦长|AB|≥2
,故弦心距d=
≤1,
即
≤1,求得-
≤m≤
,
故答案为:[-
,
].
| 3 |
r2-(
|
即
| |0-0+m| | ||
|
| 2 |
| 2 |
故答案为:[-
| 2 |
| 2 |
点评:本题主要考查直线和圆相交的性质,弦长公式、点到直线的距离公式的应用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 一个多面体的三视图如图所示,其中正视图是正方形,侧视图是等腰三角形,则该几何体的表面积为( )
一个多面体的三视图如图所示,其中正视图是正方形,侧视图是等腰三角形,则该几何体的表面积为( )| A、158 | B、108 |
| C、98 | D、88 |
在平面直角坐标系中,定点M(1,0),两动点A,B在双曲线x2-3y2=3的右支上,则cos∠AMB的最小值是( )
A、-
| ||
B、
| ||
C、-
| ||
D、
|

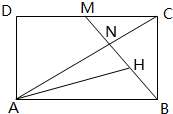 如图,M是矩形ABCD的边CD上的一点,AC与BM相交于点N,BN=
如图,M是矩形ABCD的边CD上的一点,AC与BM相交于点N,BN=