Question

【题目】已知函数的图象与x轴交点为，与此交点距离最小的最高点坐标为.

（Ⅰ）求函数的表达式；

（Ⅱ）若函数满足方程，求方程在内的所有实数根之和；

（Ⅲ）把函数的图像的周期扩大为原来的两倍，然后向右平移个单位，再把纵坐标伸长为原来的两倍，最后向上平移一个单位得到函数的图像．若对任意的，方程在区间上至多有一个解，求正数k的取值范围.

Answer 1

【答案】（Ⅰ）（Ⅱ）（Ⅲ）

【解析】

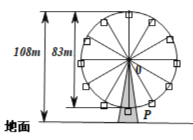
（Ⅰ）依题意作出部分函数图像，由最大值确定A，周期确定，特殊点确定即可求出解析式；（Ⅱ）由周期知在内恰有2个周期，则方程有四个根，结合图像利用对称轴即可求出所有根的和；（Ⅲ）根据三角函数的图像变化，数形结合即可得到结论.

（Ⅰ）从图知，函数的最大值为1，则，

函数的周期为，而，则

又时，，，，

解得，而，则，

∴函数的表达式为.

（Ⅱ）的周期为，

在内恰有2个周期，

并且方程在内有4个实根设为，

结合图像知.

故所有实数之和为.

（Ⅲ）先把的图像的周期扩大为原来的两倍，得到，然后向右平移个单位得到，纵坐标伸长为原来的2倍再向上平移1个单位得到，

函数的图象如图所示，

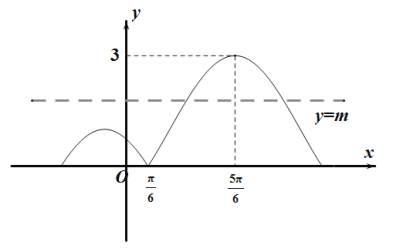
则当图象伸长为原来的5倍以上时符合题意，所以.